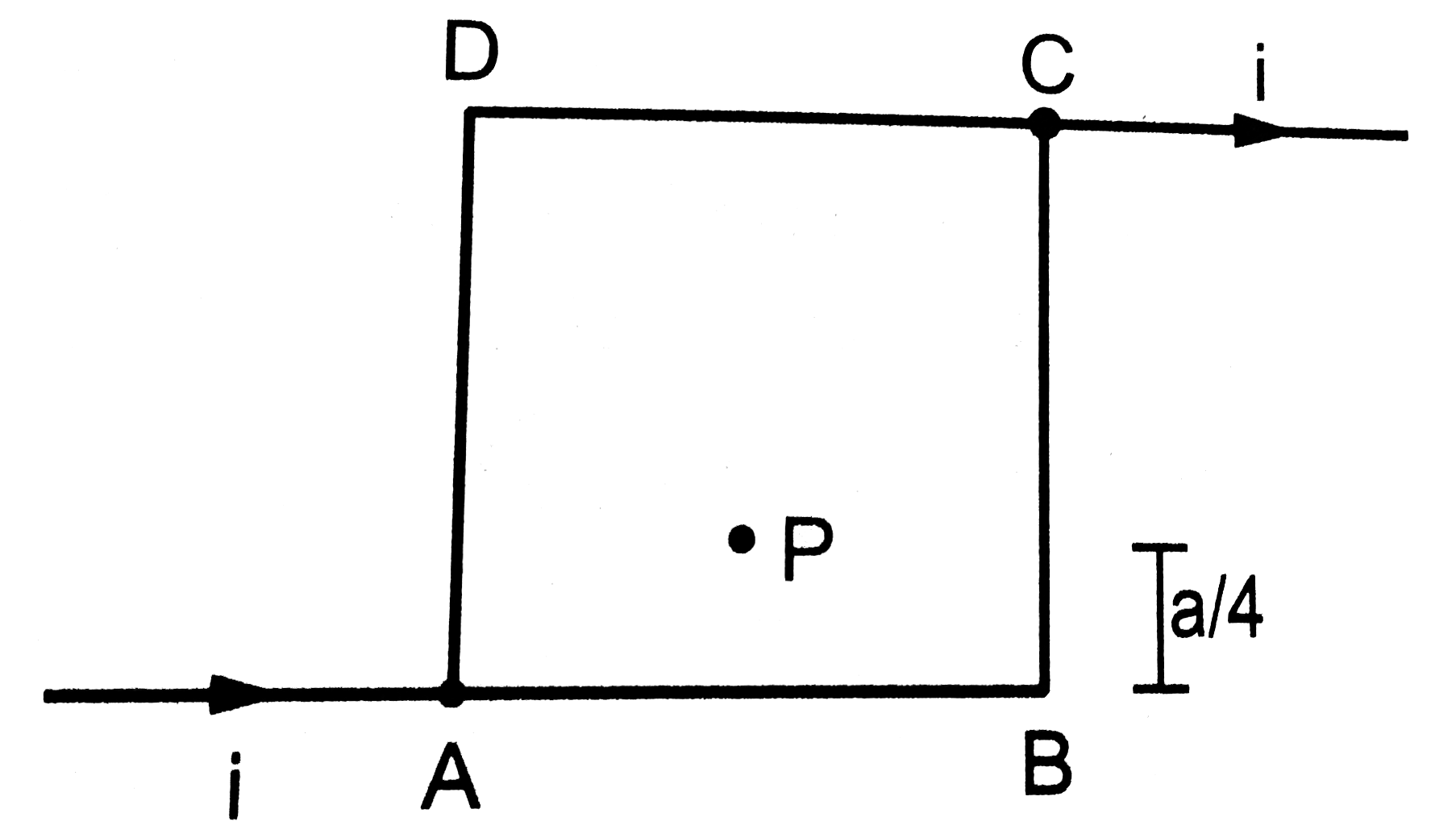
Figure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
 Solution in Tamil
Solution in Tamil
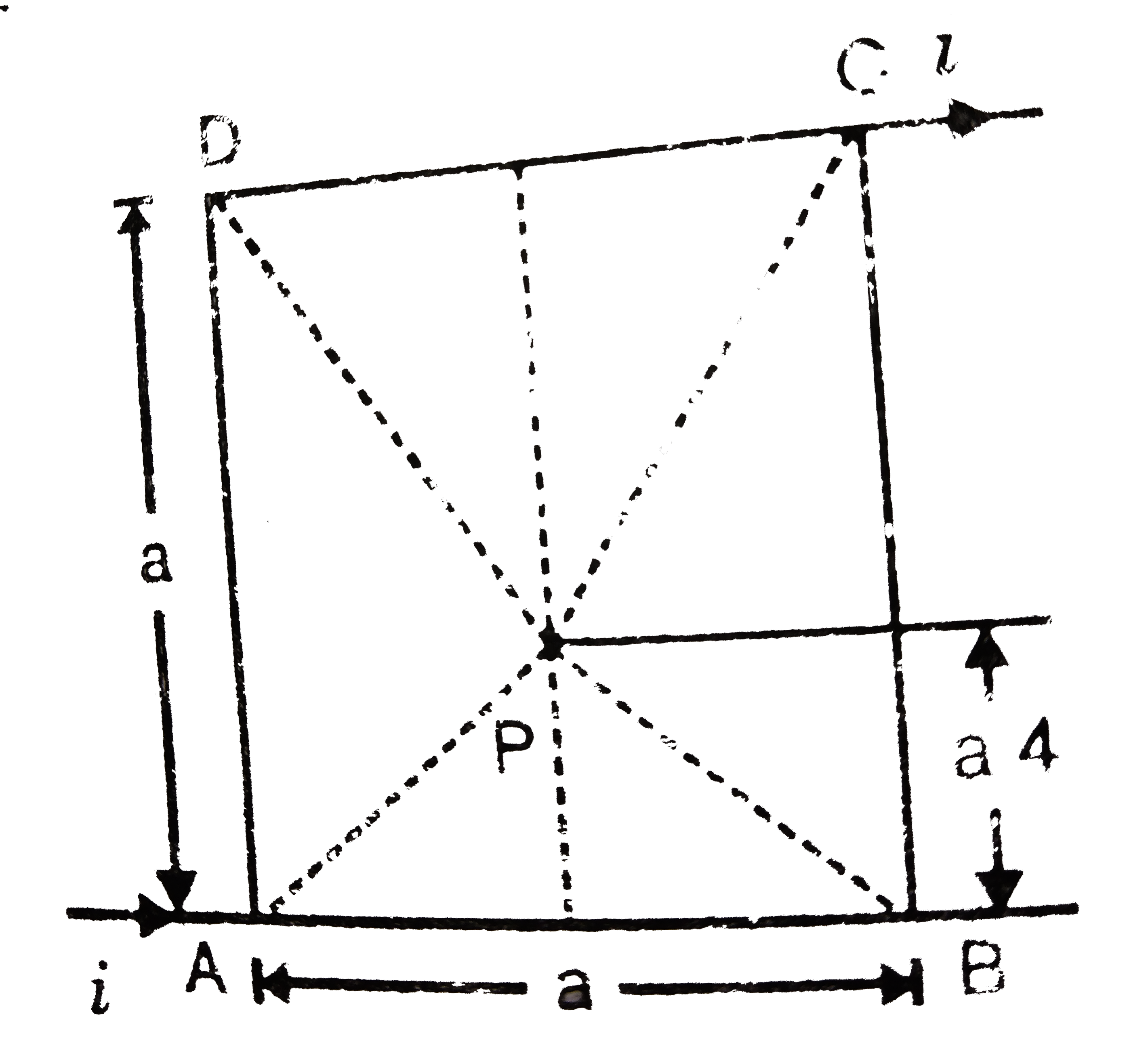
B at P due to AD =μo4π.i2.4a2.a⎡⎢
⎢
⎢
⎢⎣(a2)√(a2)2+(a4)2+(a2)√(a2)2+(3a4)2⎤⎥
⎥
⎥
⎥⎦along
=μoi2πa⎡⎢
⎢
⎢
⎢⎣(a2)√(a2)2+(a4)2+(a2)√(a2)2+(3a4)2⎤⎥
⎥
⎥
⎥⎦ along<br>BatPdue→AC=(mu_o)/(4pi).(i)/(2). (16)/(9a^2.a 2.[(((3a)/(4)))/(sqrt(((3a)/(4))^2 + ((a)/(2))^2))<br>(4mu_oi)/(9pia) [(((3a)/(4)))/(sqrt(((a)/(4))^2 +((3a)/(2))^2))]along<br>B at P due to AB = (mu_oi)/(4pi).(i)/(2) . (16)/(9a^2). a. 2 [(((a)/(4)))/sqrt(((a)/(4))^2 + ((a)/(2))^2 along<br>BatPdue→BC = (mu_o)/(4pi).(i)/(2). (4)/(a^2).a. [(((a)/(2)))/ sqrt(((a)/(2))^2 + ((a)/(2))^2) +(((a)/(2)))/sqrt(((a)/(2))^2 + ((3a)/(4))^2)] along<br>=(um_oi)/(2pia)[(((a)/(2)))/sqrt(((a)/(2))^2 +((a)/(2))^2) + (((a)/(2)))/(sqrt(((a)/(2))^2 +((3a)/(4))^2))]along⊗<br>so,net B=4μoiπa⎡⎢
⎢
⎢
⎢⎣(a4)√(a2)2+(a4)2⎤⎥
⎥
⎥
⎥⎦−4μoi9πa⎡⎢
⎢
⎢
⎢⎣(3a4)√(a2)2+(3a4)2⎤⎥
⎥
⎥
⎥⎦
=4μoiπa.14⎡⎢
⎢⎣1√14+116−4μoi9πa.34⎡⎢
⎢⎣1√14+916⎤⎥
⎥⎦
=4μoiπa[4√5]−μoi3πa[4√13][4√13]along
=4μoi2πa[1√5−13√13]along=2πoiπa[1√5−13√13]along.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
60 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercise
9 Videos
Similar Questions
The magnetic field at the origin due to a current element I (→dl)placedataposi→n(→r)is
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View SolutionThe magnetic intensity H at the centre of a long solenoid carrying a current of 2.0A, is found to be 1500Am−1. Find the number of turns per centimetre of the solenoid.
View SolutionFigure shows a square loop made from a uniform
wire. Find the magnetic field at the centre of the square
if a battery is connected between the points A and C.

View SolutionConsider the situation described in the previous problem. Suppose the current I enters the loop at the point A and leaves it at the point B. Find the magnetic field at the centre of the loop.
View SolutionA square loop of wire, edge length a, carries a current i. Compute the magnitude of the magnetic field produced at a point on the axis of the loop at a distance x from the centre.
View SolutionFigure shows a square loop made from a uniform wire. Find the magnetic field at the centre of the square if a battary is connected between points A and C.

View SolutionCurrent I enters at A in a square loop of uniform resistance and leaves at B. The ratio of magnetic field at E, the centre of square, due to segment AB to that due to DC is

View SolutionABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D. The magnetic field is
View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop

View SolutionIn the figure, the current l enters the circular loop of uniform wire of radius r at A and leaves it at B. The magnetic field of the centre of circular loop is

View SolutionThere is one circular loop of a uniform wire whose radius is R. Electric current I enters at one point on its circumference and leaves at a diametrically opposite point. What will be the net magnetic field intensity at the centre of the loop?
View SolutionThere is a circular loop of current of radius , as shown in figure: If current enters at point A and leaves at point B where angle AOB " is " 90^(@) and the wire of the loop is of uniform cross section area, then calculate the magnetic field intensity at the centre of the loop.
View SolutionABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D . The magnetic field is :

View SolutionPQRS समरूप चालक तार से बना हुआ एक वर्गाकार लूप है। चित्रानुसार बिन्दु P पर धारा प्रवेश करती है तथा O से बाहर निकलती है। तब चुम्बकीय क्षेत्र होगा

View SolutionFigure shows a square loop made from a uniform
wire. Find the magnetic field at the centre of the square
if a battery is connected between the points A and C.

View Solution
