Find the total heat produced in the loop of the previous problem during the interval 0 to 30 s if the resistance of the loop is 4.5 mOmega.Solution in Tamil
As heat product is a scalar property:
so, net heat produced
=Ha+Hb+Hc+Hd
R=42mΩ=405×10−3Ω
(a)e=3×10−4V
i=eR=3×10−44.5×10−3
=6.7×10−2Amp.
Ha=(6.7×10−2^2)×4.5×10−3×5
Hb=Hd=0
[Sinceemfis∈ducedfor5sec]
Hc=(6.7×10−2)2×4.5×10−2×5
So,→talheat
=Ha+Hc
=2×(6.7×10−2)2×4.5×10−3×5
=2×10−4J.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise9videos
ELECTROMAGNETIC WAVES
Similar Questions
A bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
07:43View SolutionFind the dimensional formula of ε0 .
03:05View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
02:01View SolutionConsider the situation described in the previous problem. Suppose the current I enters the loop at the point A and leaves it at the point B. Find the magnetic field at the centre of the loop.
02:05View SolutionCurrent in a long current carrying wire is I=2t
A conducting loop is placed to the right of this wire. Find
a. magnetic flux ϕB passing through the loop.
b. induced emf|e| prodced in the loop.
c. if total resistance of the loop is R, then find induced current Iin in the loop.06:28View SolutionA constant current I flows through a long straight wire as shown in figure. A square loop starts moving towards righ with as constant speed v . a Find induced emf produced i the loop as a function x b. If total resistance of the loop is R , then find induced current in the loop,
03:43View SolutionA magnetic flux through a stationary loop with a resistance R varies during the time interval tau as phi=at(tau-t) . Find the amount of the generated in the loop during that time
12:59View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from t=0→t=T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.04:09View SolutionA magentic flux through a statinary loop with a resistance R varies during the tiem interval τ as Φ=at(τ−t). Find the amount of heat generated in the loop during that time. The inductance of the loop is to be neglected.
03:36View SolutionIn the previous problem, fin dthe total heat produced in the loop.
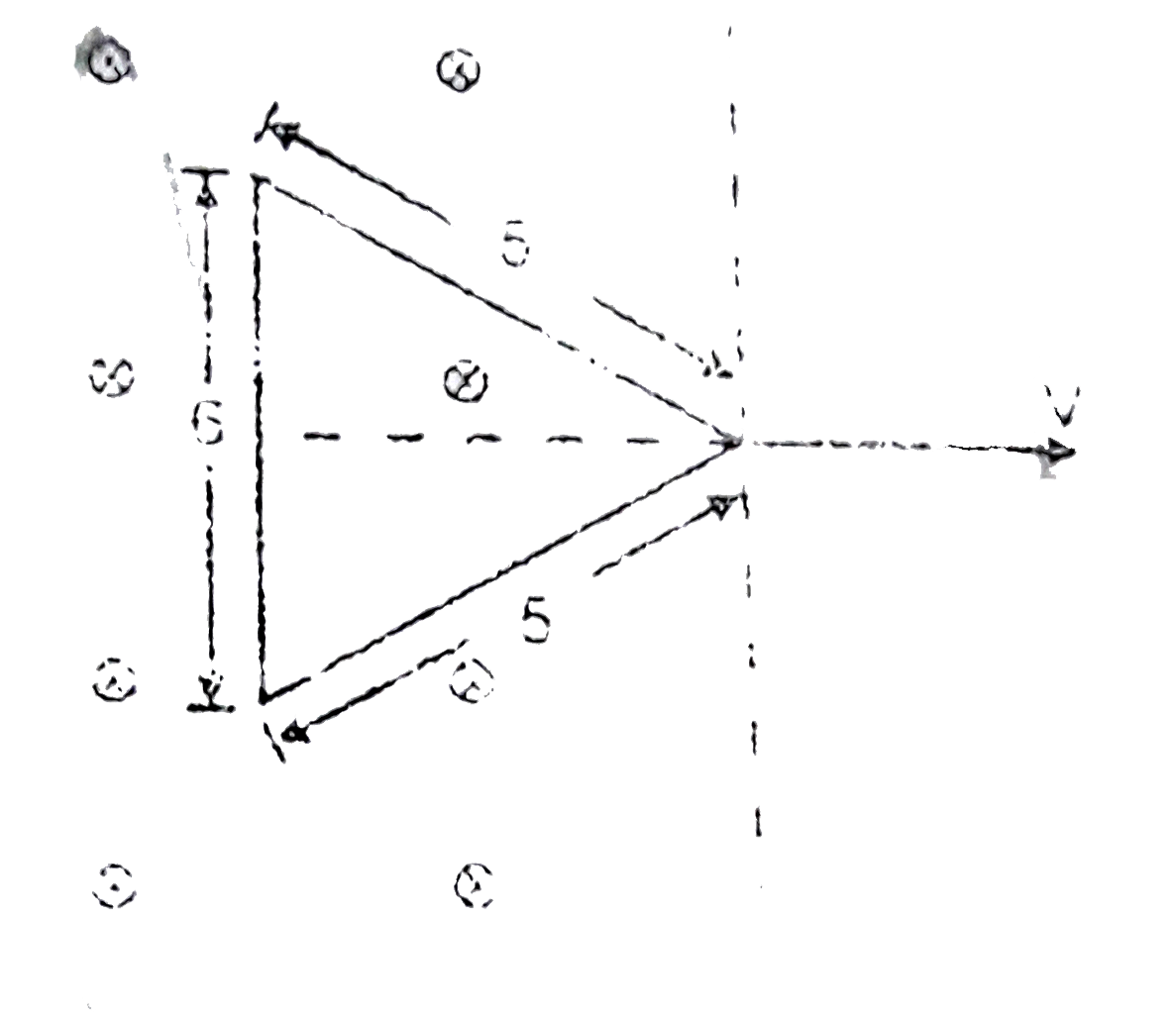
03:03View SolutionA triangle loop as shown in the figure is started to being pulled out at t=0 from a uniform magnetic field with a constant velocity v.Total resistance of the loop is constant and equals to R.Then the variation of power produced in the loop with time will be:
 40:51View Solution
40:51View SolutionMagnetic flux through a stationary loop with a resistance R varies during the time interval tau" as "phi=alphat(tau-t) where alpha is a constant. Calculate the amount of heat generated in the loop during the time interval tau .
06:13View SolutionThe magnetic flux through a stationary loop with resistance R varies during interval of time T as phi = at (T – t). The heat generated during this time neglecting the inductance of loop will be
05:22View SolutionProblems based on loop tracing
02:21View SolutionR प्रतिरोध वाले स्थायी लूप में से चुम्बकीय फ्लक्स ϕ=at(τ−t) के रूप में समय अन्तराल τ के दौरान परिवर्तित होता है। उस समय के दौरान लूप में उत्पन्न ऊष्मा की मात्रा क्या है?
07:39View SolutionA magnetic flux through a stationary loop with a resistance R varies during the time interval tau as phi = at (tau-t) What is the amount of heat generated in the loop during that time?
05:06View Solution

