A girl is observing a bird sitting at a height of 500 m from the ground. The angle of elevation of the bird from the girl's eyes is at the initial position. After some time, the girl moves on the ground towards the bird by 50 m and bird flies away from her. At this point, the angle of elevation reduces to . Find the distance travelled by the bird. Take
415 m
915 m
315 m
365 m
The correct Answer is:A
To solve the problem step by step, we will use trigonometric principles to find the distance traveled by the bird.
Step 1: Initial Setup
Let’s denote:
- The height of the bird (AB) = 500 m
- The initial position of the girl (C) is at a distance (BC) from the base of the bird (B).
- The angle of elevation from the girl to the bird at the initial position (C) is 45°.
Step 2: Using the Tangent Function
From triangle ABC, we can use the tangent of the angle of elevation:
tan(45°)=ABBC
Since tan(45°)=1:
1=500BC⟹BC=500 m
Step 3: Girl Moves Towards the Bird
After moving 50 m towards the bird, the new position of the girl is F. Therefore, the new distance from the bird (BF) is:
BF=BC−50=500−50=450 m
Step 4: New Angle of Elevation
At this new position (F), the angle of elevation to the bird is now 30°. We can again use the tangent function:
tan(30°)=ABBF+y
Where y is the distance the bird has moved away from its original position.
Step 5: Substitute Values
Since tan(30°)=1√3:
1√3=500450+y
Step 6: Cross-Multiply
Cross-multiplying gives:
450+y=500√3
Step 7: Substitute √3
Using the given value √3=1.73:
450+y=500×1.73
Calculating the right side:
450+y=865
Step 8: Solve for y
Now, solving for y:
y=865−450=415 m
Conclusion
The distance traveled by the bird is 415 m.
---
Let’s denote:
- The height of the bird (AB) = 500 m
- The initial position of the girl (C) is at a distance (BC) from the base of the bird (B).
- The angle of elevation from the girl to the bird at the initial position (C) is 45°.
From triangle ABC, we can use the tangent of the angle of elevation:
tan(45°)=ABBC
Since tan(45°)=1:
1=500BC⟹BC=500 m
After moving 50 m towards the bird, the new position of the girl is F. Therefore, the new distance from the bird (BF) is:
BF=BC−50=500−50=450 m
At this new position (F), the angle of elevation to the bird is now 30°. We can again use the tangent function:
tan(30°)=ABBF+y
Where y is the distance the bird has moved away from its original position.
Since tan(30°)=1√3:
1√3=500450+y
Cross-multiplying gives:
450+y=500√3
Using the given value √3=1.73:
450+y=500×1.73
Calculating the right side:
450+y=865
Now, solving for y:
y=865−450=415 m
The distance traveled by the bird is 415 m.
Similar Questions
An observer 1.5 m tall is 28.5 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45o.What is the height of the chimney?
View SolutionA bird is sitting on the top of an 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45∘. The bird flies away horizontally in such a way that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30∘. Find the speed of flying of the bird. (Take √3=1.732).
View Solution
Knowledge Check
From a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ . The height of the tower is
A10√3mB20√3 mC10√3 mD20√3mAn observer who is 1.62m tall is 45m away from a pole . The angle of elevation of the top of the pole from his eyes is 30∘. The height ( in m ) of the pole is closest to :
A26.2B27.6C25.8D26.8
An observer 1.5 m tall is 28.5 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45∘. What is the height of the chemney ?
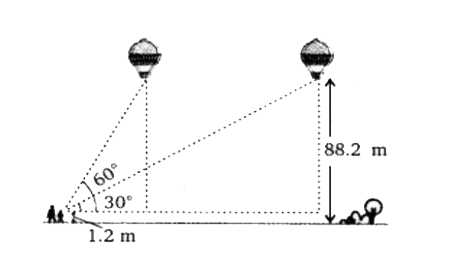
View SolutionA 1.2 m tall girl spots a ballon moving with wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60∘. After some time, the angle of elevation reduces to 30∘. Find the distance travelled by the balloon during the interval.
View SolutionFrom a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘. The angle of elevation of the top of a water tank(on the top of tower) is 45∘.find the height of the tower and depth of tank
View SolutionA person standing at a distance of 90 m from a church observes the angle of elevation of its top to be 45∘ . Find the height of the chruch .
View SolutionA 1.2m tall girl spots a balloon moving with the wind in a horizontal line at a height 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°.After sometime, the angle of elevation reduces 30°.Find the distance travelled by the balloon during the interval.
View SolutionFrom a point on the ground 20 m away from the foot of a tower the angle of elevation is 60∘. What is the height of tower?
View Solution
