In the following questions, a series is given with one term missing. Choose the correct alternative form the given ones that will complete the series.
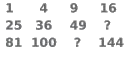
64 & 121
20 & 100
121 & 46
95 & 150
The correct Answer is:A
The given numbers are the squares of natural numbers starting from .1. .
Hence, missing numbers are squares of 8 and 11 i.e 64 and 121.
Hence, option A is the correct answer.
Similar Questions
In the following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.

View SolutionIn the following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.

View Solution
Knowledge Check
In following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
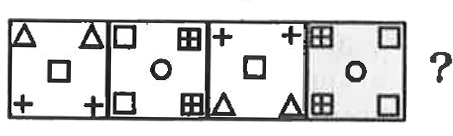 A
A B
B C
C D
D
In following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
 A
A B
B C
C D
D
In following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
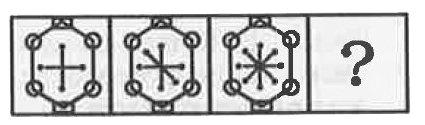 A
A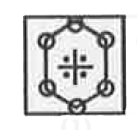 B
B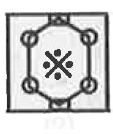 C
C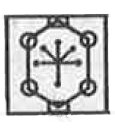 D
D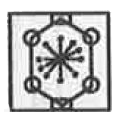
In the following question, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.

View SolutionIn following questions, a series is given with one term missing. Choose the correct alternative from the given ones that will complete the series.
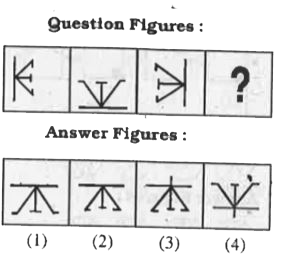
View SolutionIn the following questions, a series is given, with one term missing. Choose the correct alternative from the given ones that will complete the series.
NOABOPBCPQCD ? ? ? ?
View SolutionIn the following questions, a series is given, with one term missing. Choose the correct alternative from the given ones that will complete the series.
WVTSOPNMKJ ? ?
View SolutionIn the following questions, a series is given, with one term missing. Choose the correct alternative from the given ones that will complete the series.
WTPMIFB ____,_____
View Solution
