A cyclist moves at an angle with the vertical along the road. He moves with speed v describing a certain angle, the angle being small. If the speed changes to 2u, then the angle in this case bears a ratio with the former angle:
4:1
1:4
1:2
2:1
The correct Answer is:A
Here letθ1, and θ2 be the angles at which the cyclist bends, then
tanθ2tanθ1=(22v)2r.g×r.gv2=41
Topper's Solved these Questions
- UNIFORM CIRCULAR MOTIONBOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Recent Competitive Questions
3 Videos
- UNIFORM CIRCULAR MOTIONBOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Revision Test
57 Videos
- UNIFORM CIRCULAR MOTIONBOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Multiple Choice Questions(LEVEL II )
1 Videos
- TRANSFERENCE OF HEAT BOOK - MODERN PUBLICATIONCHAPTER - TRANSFERENCE OF HEAT EXERCISE - Recent Competitive Questions
4 Videos
- UNIT TEST -06BOOK - MODERN PUBLICATIONCHAPTER - UNIT TEST -06EXERCISE - Multiple Choice Questions
19 Videos
Similar Questions
Knowledge Check
Aparticle moves with a speed v changes direction by an angle θ, without change in speed.
Athe change in the magnitude in velocity is zeroBthe change in the magnitude fo its velocity is 2vsinθ/2Cthe magnitude of change in velcoity is 2vsinθ/2Dthe magnitude of change in velocity is v(1−cosθ)A particle moving with a speed v changes direction by an angle θ, without change in speed.
AThe change in the magnitude of its velocity is zeroBThe change in the magnitude of its velocity is 2vsin(θ/2)CThe magnitude of the change in its velocity is 2vsin(θ/2)DThe magnitude of the change in its velocity is v(1−cosθ)A particle is thrown with a speed is at an angle θ with the horizontal. When the particle makes an angle ϕ with the horizontal, its speed changes to v, then
Av=v0cosθBv=v0cosθ⋅cosϕCv=v0cosθ⋅secϕDv=v0secθ⋅cosϕ
A particle is projected at an angle θ with an initial speed u.
View SolutionA particle is thrown with a speed u at an angle θ with the horizontal. When the particle makes an angle ϕ with the horizontal. Its speed changes to v :
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ with the vertical, and rebounds with a speed υ, at an angle ϕ with the vertical. The coefficient of restitution between the particle and the floor is e. The angle ϕ is equal to :
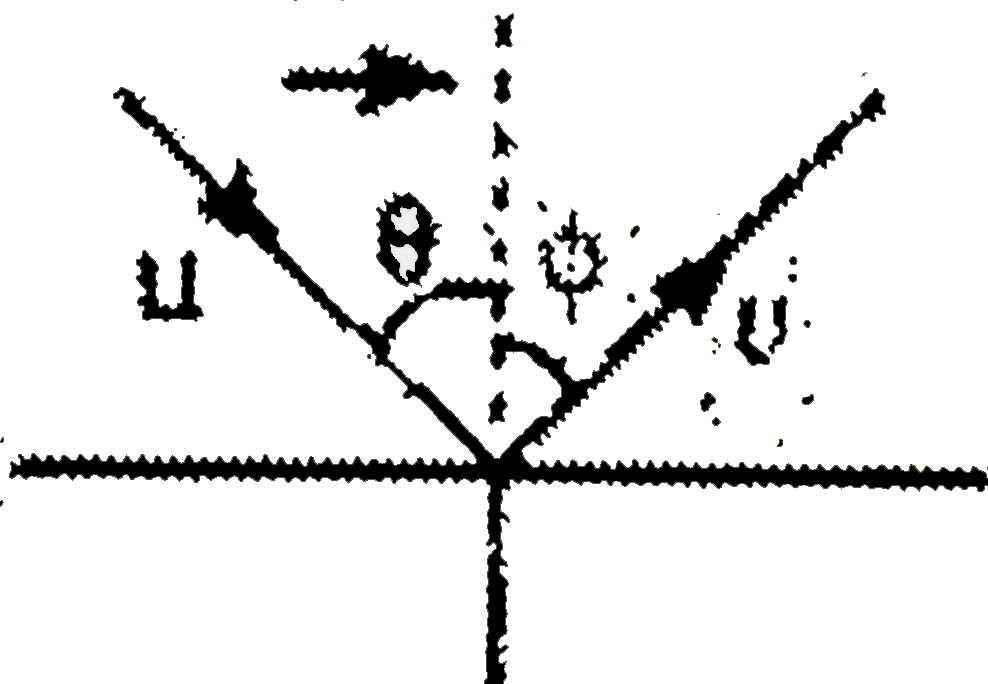
View SolutionA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The angle ϕ is equal to
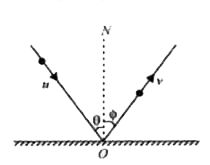
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ to the vertical, and rebounds with a speed v, at an angle ϕ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is
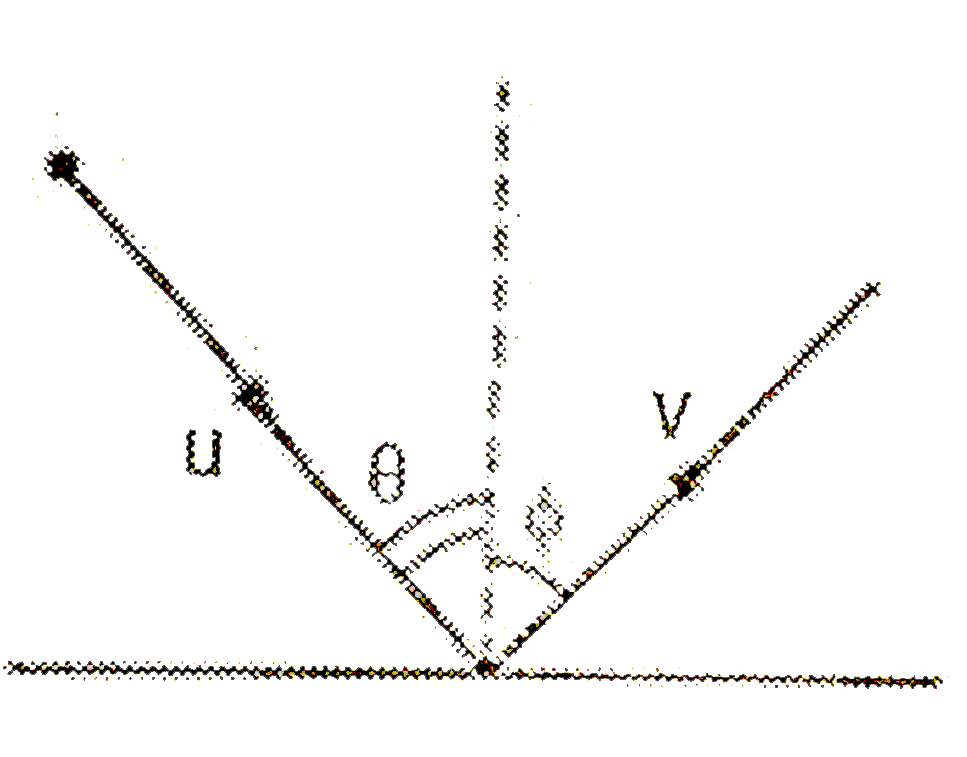
View Solution
