An annular ring with inner and outer radii Rand R is rolling without slipping with uniform angular speed 00. The ratio of the forces experienced by the two particles situated at the inner and outer parts of the ring i.e. is :
1
The correct Answer is:D
Here
Topper's Solved these Questions
- UNIFORM CIRCULAR MOTIONBOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Recent Competitive Questions
3 Videos
- UNIFORM CIRCULAR MOTIONBOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Revision Test
57 Videos
- UNIFORM CIRCULAR MOTIONBOOK - MODERN PUBLICATIONCHAPTER - UNIFORM CIRCULAR MOTIONEXERCISE - Multiple Choice Questions(LEVEL II )
1 Videos
- TRANSFERENCE OF HEAT BOOK - MODERN PUBLICATIONCHAPTER - TRANSFERENCE OF HEAT EXERCISE - Recent Competitive Questions
4 Videos
- UNIT TEST -06BOOK - MODERN PUBLICATIONCHAPTER - UNIT TEST -06EXERCISE - Multiple Choice Questions
19 Videos
Similar Questions
An annular ring with inner and outer radii R1 and R2 is rolling wihtout slipping with a uniform angular speed. The ratio of the forces experienced by the two particles situated on the inner and outer parts of the ring, F1F2 is
View SolutionAn annular ring with inner and outer radii R1 and R2 is rolling wihtout slipping with a uniform angular speed. The ratio of the forces experienced by the two particles situated on the inner and outer parts of the ring, F1F2 is
View Solution
Knowledge Check
An annular ring with inner and outer radii R1 and R2 is rolling wihtout slipping with a uniform angular speed. The ratio of the forces experienced by the two particles situated on the inner and outer parts of the ring, F1F2 is
A(a) (R1R2)2B(b) R2R1C(c) R1R2D(d) 1The figure shows a system consisting of (i) a ring the outer radius 3R rolling clockwise without slipping on a horizontal surface with angular speed ω and (ii) an inner disc of radius 2R rotating anti clockwise with angular speed ω/2. The ring and disc are separated. The point P on the inner disc is at a distance R from the origin, where OP makes an angle of 30∘ with the horizontal. Then with respect to the horizontal surface,
Athe point O has linear velocity 3RωˆiBthe point P has linear velocity 114Rωˆi+√34Rωˆk.Cthe point P has linear velocity 134Rωˆi−√34RωˆkDthe point P has linear velocity ((3−√34)Rωˆi+14Rωˆk.
An angular ring wth inner and outer radii R1=1.2cm and R2=4.8cm is rolling without slipping with a unifrom angular speed. What is the ratio of the forces experienced by the two particles of same mass situted on the outher and inner parts of the annular ring ?
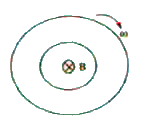
View SolutionAn annular disc of copper with inner and outer radii r and R is rotating with a uniform angular speed w in a region where a uniform magnetic field B exists as shown. Then net emf induced between the inner edge and outer edge of the disc is
View SolutionTwo bodies a ring and a solid cylinder of same material are rolling down without slipping an inclined plane. The radii of the bodies are same. The ratio of velocity of the centre of mass of the bottom of the inclined plane of the ring to that of the cylinder is √x2 . Then, the value of x is ……………….
View Solution1 If r and R be the radii of inner and outer circles respectively, then area of ring is
View SolutionThe radii of three concentric circles are in the ratio 1:2:3. Find the ratio of the area between the two inner circles to that between the two outer circles.
View SolutionThe figure shows a system consisting of (i) a ring the outer radius 3R rolling clockwise without slipping on a horizontal surface with angular speed ω and (ii) an inner disc of radius 2R rotating anti clockwise with angular speed ω/2. The ring and disc are separted. The point P on the inner disc is at a distance R from the origin, where OP makes an angle of 30∘ with the horizontal. Then with respect to the horizontal surface,
View Solution
