Consider a block of conducting material of resistivity p shown in the figure. Current l enters at A and leaves from D. We apply superposition principle to find voltage ΔV developed between B and C.
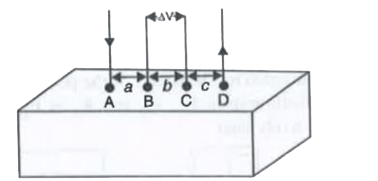
The calculation is done in the following steps :
(a) Take current I entering from A and assume it to spread over a hemispherical surface in the block.
(b) Calculate field E (r) at distance r from A by using Ohm's law E = pj, where j is the current per unit area at r.
(c) From the r dependence ofE (r), obtain the potential V (r) at r.
(d) Repeat (I), (ii) and (iii) for current l leaving D and superpose results for A and D.
For current entering at A, the electric field at a distance r from A is
pI4πr2
pI8πr2
pIr2
pI2πr2
The correct Answer is:D
E=pJ=pI2πr2
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - MULTIPLE CHOICE QUESTIONS (LEVEL-II)
8 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - MULTIPLE CHOICE QUESTIONS (LEVEL-III)
13 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - MULTIPLE CHOICE QUESTIONS ( LEVEL-II)
54 Videos
- ATOMS, MOLECULES AND NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEIEXERCISE - Recent Competitive Questions
40 Videos
- DESCRIPTION OF MOTION IN ONE DIMENSION BOOK - MODERN PUBLICATIONCHAPTER - DESCRIPTION OF MOTION IN ONE DIMENSION EXERCISE - Revision Test
45 Videos
Similar Questions
Passage-II:
Consider a block conducting material of resistivity .ρ. shown in the figure. Current .I. enters at .A. and leaves from .D.. We apply superposition principle to find voltage .ΔV. developed between .B. and .C.. The calculation is done in the following steps :
i) Take current .I. entering from .A. and assume it to spread over a hemispherical surface in the block.
ii) Calculate field E(r ) at distance .r. from A by using Ohm.s law E=ρj, where j is the current per unit area at .r..
iii) From the .r. dependence of E(r ), obtain the potential V(r ) at r.
iv) Repeat (i), (ii), (iii) for current .I. leaving .D. and superpose results for .A. and .D..
For current entering at A the electric field at a distance .r. from A is
View SolutionConsider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
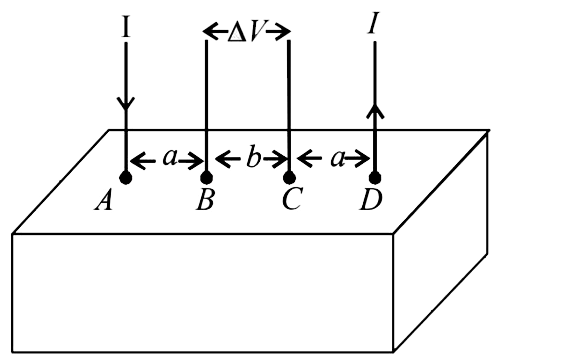
Delta V measured between B and C is
View Solution
Knowledge Check
Consider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
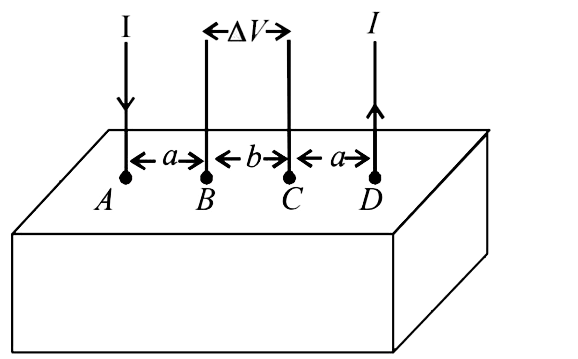
For current entering at A, the electric field at a distance 'r'AρI8πr2BρIr2CρI2πr2DρI4πr2Consider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
Delta V measured between B and C isAρIπa−ρIπ(a+b)BρIa−ρIa+bCρI2πa−ρI2π(a+b)DρI2π(a−b)ABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D. The magnetic field is
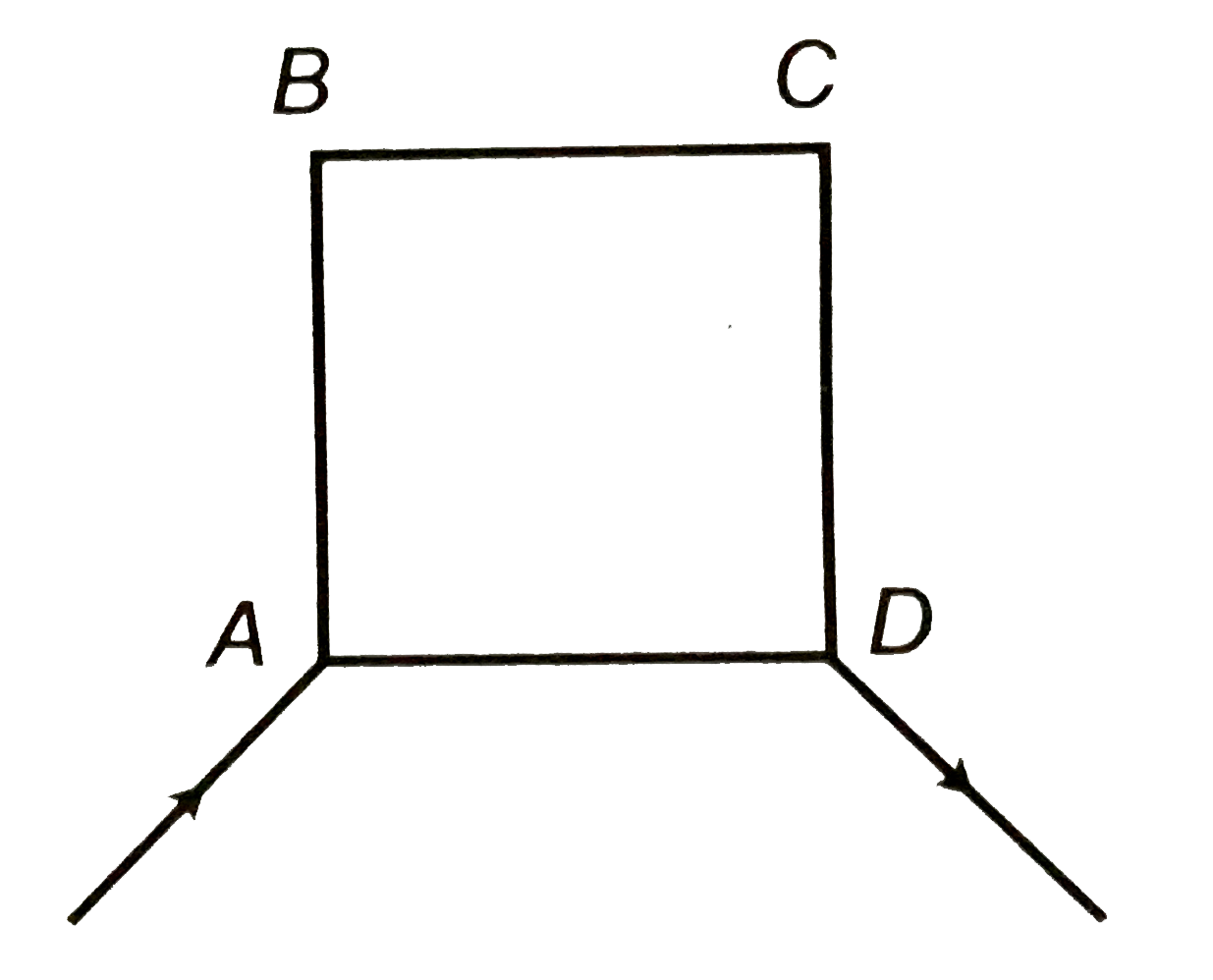Azero only at the centre of the loopBmaximum at the centre of the loopCzero at all point outside the centre loopDzero at all points inside the loop
When some potential differece is maintained between A and B, current I enters the network at A and leaves at B
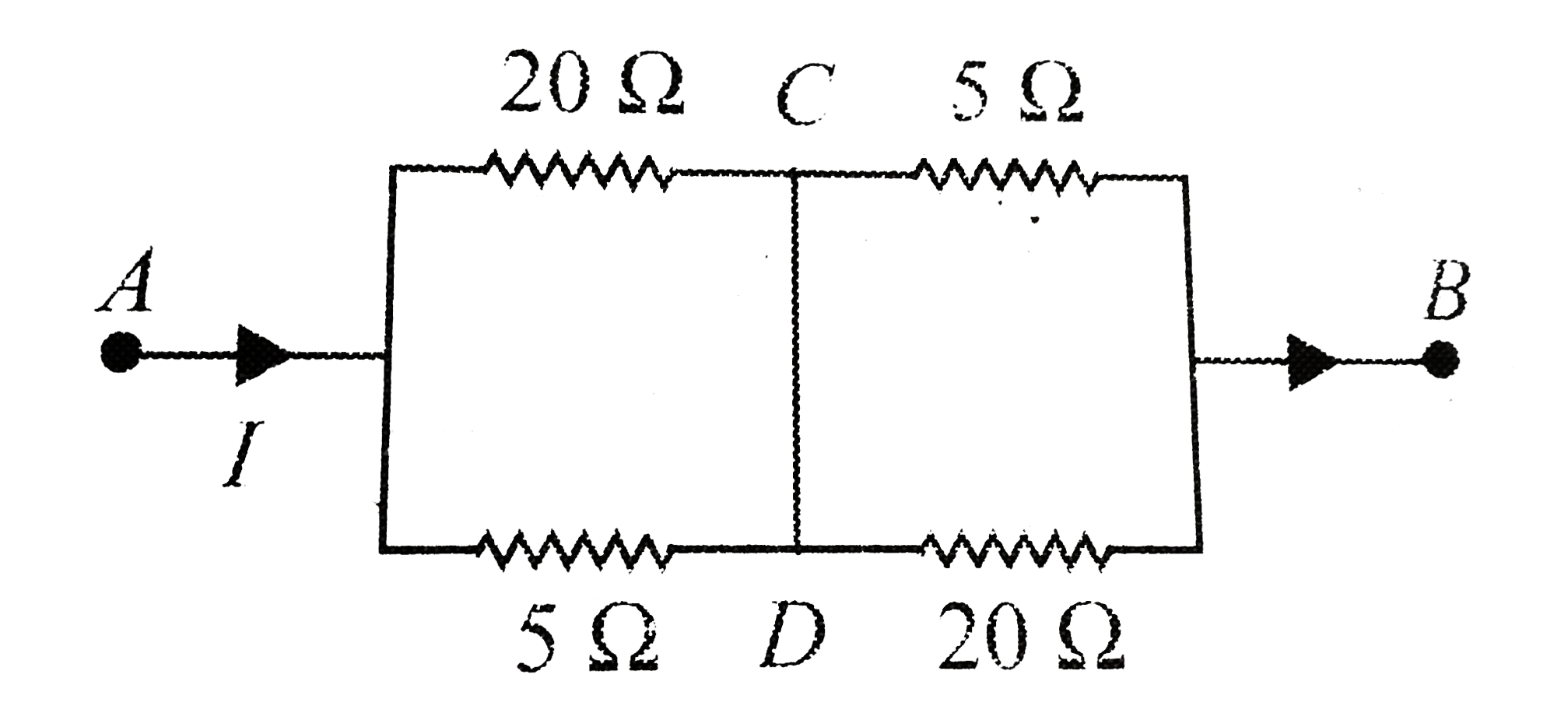
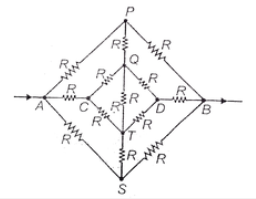
View SolutionA current enters from A and leaves at B through the network shown. Select the correct alternative(s).
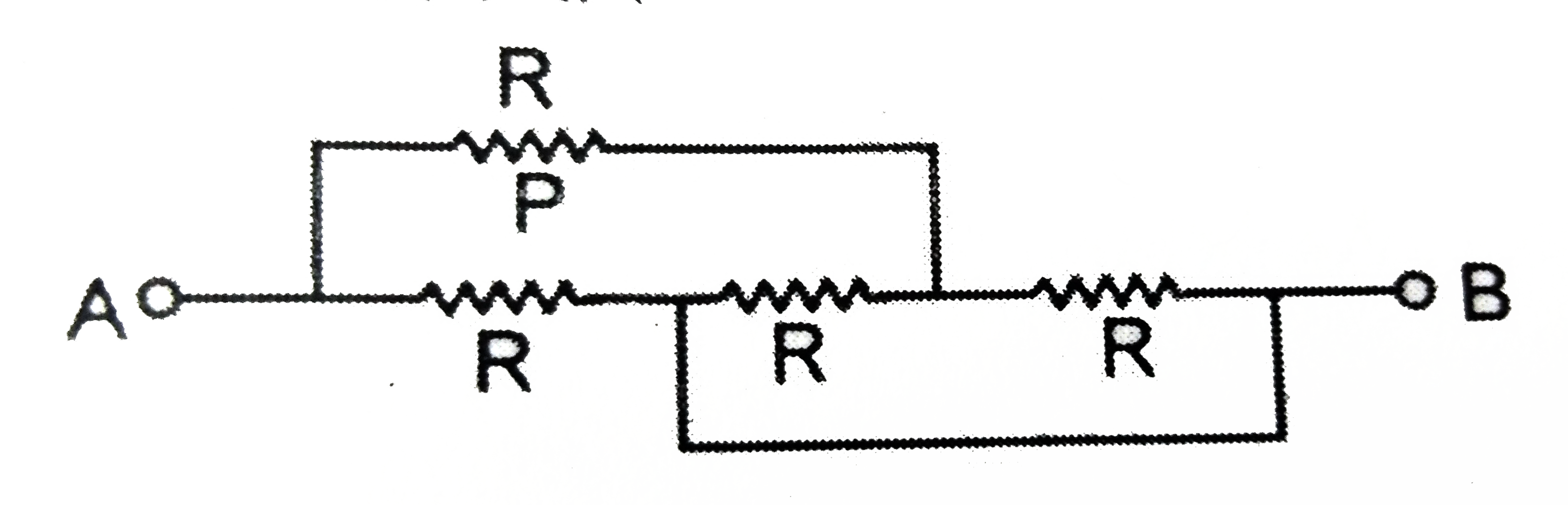
View SolutionFind the current in Resistance P if voltage supply between A and B volts.
View SolutionWhen some potential differece is maintained between A and B, current I enters the network at A and leaves at B
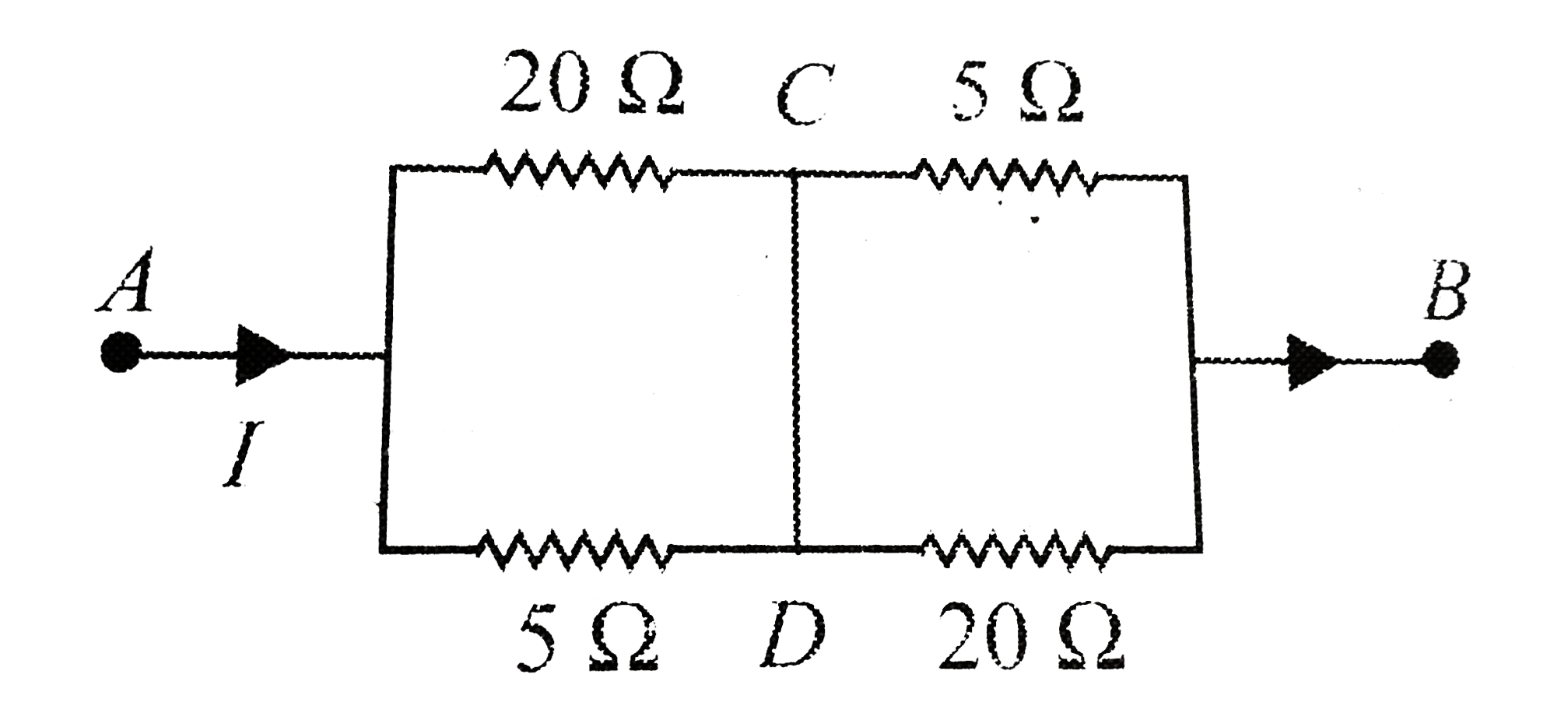
View SolutionThere is a circular loop of current of radius , as shown in figure: If current enters at point A and leaves at point B where ∠AOB is 90∘ and the wire of the loop is of uniform cross section area, then calculate the magnetic field intensity at the centre of the loop.
View Solution