Ten persons numbered 1, ,2 ..,10 play a chess tournament, each player against every other player exactly one game. It is known that no game ends in a draw. If are the number of games won by players 1, ,2 3, ...,10, respectively, and are the number of games lost by the players 1, 2, ...,10, respectively, then Solution in Kannada
None of these
The correct Answer is:C
Clearly, each player will play 9 games.
Total number of games=
clearly,
.
Similar Questions
शतरंज के टूर्नामेंट में दो महिलाएँ भाग लेती है। प्रत्येक खिलाडी, दुसरे खिलाडियों के साथ दो गेम खेलती है | पुरुषो तथा पुरुषो के बीच खेले गए गेम की संख्या, पुरुषो तथा महिलाओं के बीच खेले गए गेम की संख्या से 66 अधिक है, तो खिलाडियो कि कुल संख्या होगी
View Solution10 व्यक्तियों को 1 से 10 तक की संख्याओं द्वारा दर्शाया जाता है वे एक शतरंज प्रतियोगिता में भाग लेते है प्रत्येक खिलाड़ी प्रत्येक दूसरे खिलाड़ी के साथ एक खेल पूर्णतः खेलता है किसी भी खेल को ड्रा से खत्म नहीं किया जाता है। खिलाड़ियों 1, 2, 3, ..., 10 के द्वारा जीते गये खेलों की संख्या कमशः w1,w2,....,w10 तथा हारे गए खेलों की संख्या l1,l2,...,l10 क्रमानुसार हो, तो
View SolutionIn a chess tournament where the participants were to play one game with another, two players fell ill having played 3 games each. If the total number of games played is 84, the number of participants at the beginning was
View SolutionFollowing table shows the points of scores each player plays: Player Game 1 Game 2 Game 3 Game 4 A 14 16 10 10 B 0 8 6 4 C 8 11 Did not play 13 Find the average scores of three players. Who is the best performer?
View SolutionIn a badminton tournament each player played one game with all the other players. How many players participated in the touinament if they played 105 games in all?
View SolutionThe adjoining diagram shows a pie-chart with central angles for number of players playing four games A, B, C and D. If each player takes part in only one game and there are 480 players in all, find :
(i) how many players play the game D?
(ii) how many players do not play game B?
(iii) what is the ratio of players playing game A to the players playing game C ?
(iv) what percentage of players are playing game B?
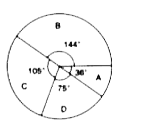
View SolutionIn a badminton each player played one game with ll the other players. Number of players participated in the tournament if they played 105 games is
View SolutionIn a class tournament where the participants were to play one game with one another, two of the class players fell ill, having played 3 games each. If the total number of games played is 24, then the number of participants at the beginning was
View Solution
