If S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.Solution in Kannada
Clearly, by triangle law of addition, we have

PQ+QS=PS . . . (i)
and PR+RS=PS . . . (ii)
On adding Eqs. (i) and (ii), we get
(PQ+QS)+(PR+RS)=2PS
⇒(PQ+PR)+(QS+RS)=2PS
⇒PQ+PR+0=2PS
[∵ S is mid-point of QR∴QS=−RS]
Hnce, PQ+PR=2PS Hence, proved.
Similar Questions
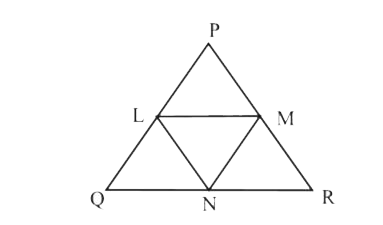
In the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
View SolutionIn ΔPQR,PQ=PR=18cm, AB and AC are parallel to lines PR and PQ respectively. If A is the mid-point of QR, then what is the perimeter (in cm) of quadrilateral ABPC?
View Solution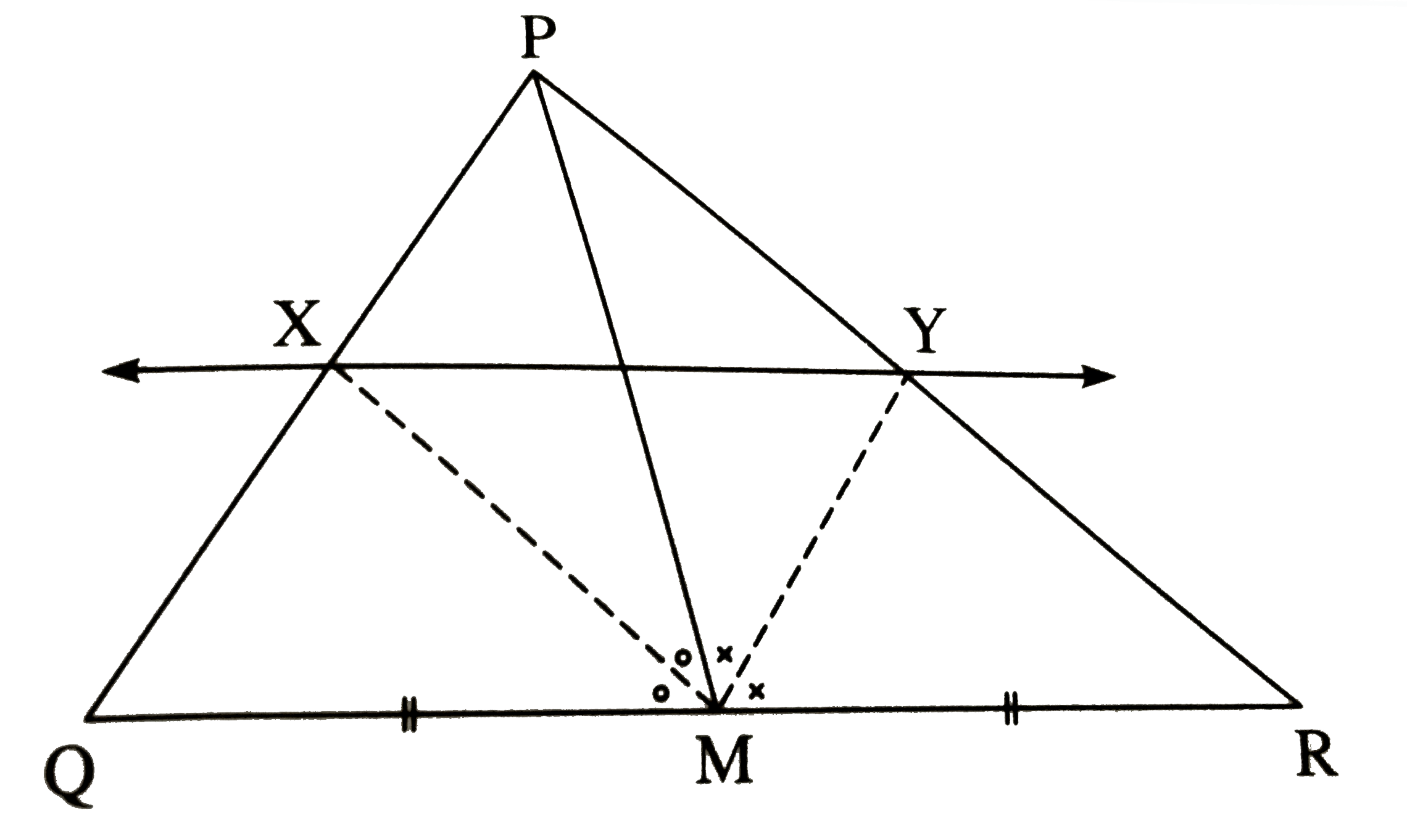
In ΔPQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR interesect sPQ and sPR in points X and Y respectively. Prove that XY∣∣QR.
View SolutionIn an isosceles triangle PQR, PQ =PR and S is any point on side QR. Then prove that: PQ2−PS2=QS×SR.
View SolutionIn ΔPQR,Pq=PR and S is the mid-point of PQ. A line drawn from S parallel to QR, intersects the line PR at T. Prove that PS = PT.
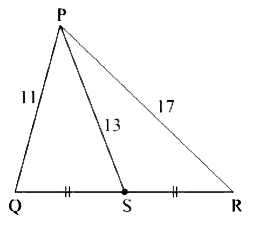
View SolutionIn ΔPQR, point S is the midoint of side QR. If PQ=11,PR=17,PS=13, Find QR.
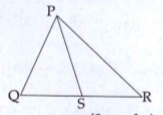
View SolutionIn the figure triangle PQR Prove that if S is any one point on the side QR, PQ+QR+RP gt 2PS
View SolutionIn the adjoining figure, point S is on side QR of ΔPQR . Prove that PQ+QR+RP>2PS
View Solution
