Question

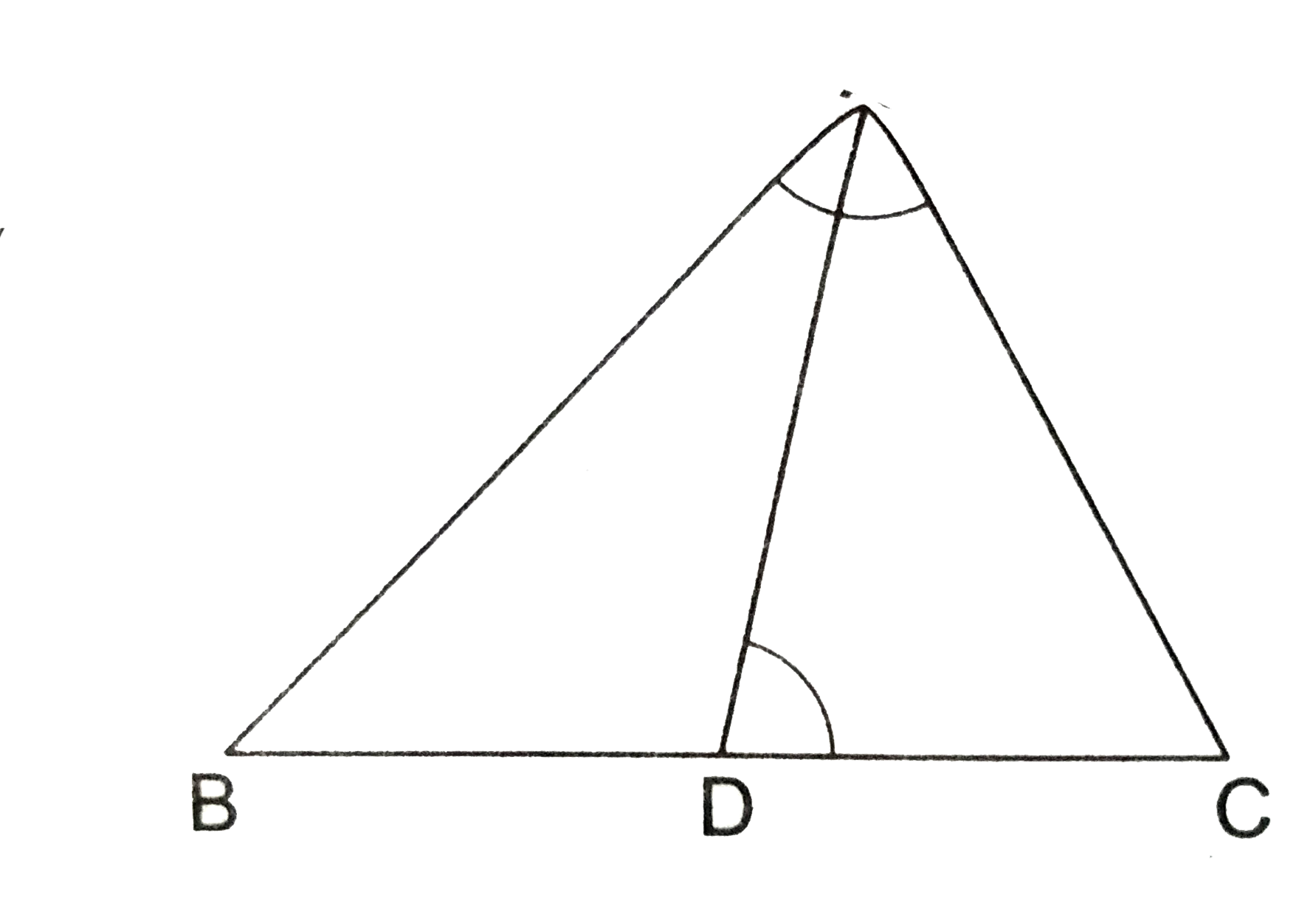
In $△ABC,D$ is point on BC such that $\angle BAD=\frac{1}{2}\angle ADC,\angle BAC={84}^{\circ }\text{and}\angle C={42}^{\circ }$. What is the measure of $\angle ADB$ ?

Options

A. `102^(@)`
B. `68^(@)`
C. `94^(@)`
D. `72^(@)`

Answer

D

Explanation

To solve the problem step by step, let's follow the reasoning laid out in the video transcript.

Step 1: Understand the given information
We have triangle ABC with:
- \( \angle BAC = 84^\circ \)
- \( \angle C = 42^\circ \)
- \( D \) is a point on \( BC \) such that \( \angle BAD = \frac{1}{2} \angle ADC \)

Step 2: Find \( \angle ABC \)
Using the property that the sum of angles in a triangle is \( 180^\circ \):
\( \angle ABC + \angle BAC + \angle C = 180^\circ \)
Substituting the known angles:
\( \angle ABC + 84^\circ + 42^\circ = 180^\circ \)
\( \angle ABC + 126^\circ = 180^\circ \)
\( \angle ABC = 180^\circ - 126^\circ = 54^\circ \)

Step 3: Set up the angles involving point D
Let \( \angle ADC = 2x \). According to the problem:
\( \angle BAD = x \)
Since \( \angle BAD = \frac{1}{2} \angle ADC \), we have:
\( \angle BAD = x \quad \text{and} \quad \angle ADC = 2x \)

Step 4: Use the exterior angle theorem in triangle ADB
In triangle ADB, the exterior angle \( \angle ADC \) is equal to the sum of the two opposite interior angles:
\( \angle ADC = \angle ADB + \angle ABD \)
Substituting the known values:
\( 2x = \angle ADB + 54^\circ \)

Step 5: Solve for \( x \)
From the equation \( 2x = \angle ADB + 54^\circ \), we can express \( \angle ADB \) as:
\( \angle ADB = 2x - 54^\circ \)

Step 6: Find the value of \( x \)
Using the triangle ADB's interior angles, we know:
\( \angle ADB + \angle BAD + \angle ABD = 180^\circ \)
Substituting the known angles:
\( (2x - 54^\circ) + x + 54^\circ = 180^\circ \)
Simplifying:
\( 3x = 180^\circ \)
\( x = 60^\circ \)

Step 7: Find \( \angle ADB \)
Now substituting \( x \) back into the expression for \( \angle ADB \):
\( \angle ADB = 2(60^\circ) - 54^\circ \)
\( \angle ADB = 120^\circ - 54^\circ = 66^\circ \)

Step 8: Find the final angle
Now we have:
\( \angle ADB + 54^\circ + 54^\circ = 180^\circ \)
This gives:
\( \angle ADB + 108^\circ = 180^\circ \)
\( \angle ADB = 180^\circ - 108^\circ = 72^\circ \)

Thus, the measure of \( \angle ADB \) is \( 72^\circ \).

Final Answer
\( \angle ADB = 72^\circ \)