The cross product of two vectors gives null vector when the vectors enclose an angle to
90∘
180∘
45∘
120∘
The correct Answer is:B
To solve the question regarding the conditions under which the cross product of two vectors results in a null vector, we can follow these steps:
1. Understanding the Cross Product:
The cross product of two vectors A and B is given by the formula:
A×B=|A||B|sin(θ)^n
where θ is the angle between the two vectors, and ^n is the unit vector perpendicular to the plane formed by A and B.
2. Condition for Null Vector:
The cross product results in a null vector (zero vector) when:
A×B=0
This occurs when the entire expression for the cross product equals zero.
3. Analyzing the Formula:
From the equation:
|A||B|sin(θ)^n=0
Since A and B are non-zero vectors, the magnitudes |A| and |B| are not zero. Therefore, for the product to be zero, we must have:
sin(θ)=0
4. Finding Angles:
The sine function equals zero at specific angles:
sin(θ)=0whenθ=0∘,180∘,360∘,…
Thus, the angles between the vectors that lead to a null vector are 0∘ and 180∘.
5. Conclusion:
The question specifically asks for the angle that results in a null vector. Among the options provided, the angle 180∘ is a valid answer. Therefore, the answer to the question is:
The angle is 180∘.
The cross product of two vectors A and B is given by the formula:
A×B=|A||B|sin(θ)^n
where θ is the angle between the two vectors, and ^n is the unit vector perpendicular to the plane formed by A and B.
The cross product results in a null vector (zero vector) when:
A×B=0
This occurs when the entire expression for the cross product equals zero.
From the equation:
|A||B|sin(θ)^n=0
Since A and B are non-zero vectors, the magnitudes |A| and |B| are not zero. Therefore, for the product to be zero, we must have:
sin(θ)=0
The sine function equals zero at specific angles:
sin(θ)=0whenθ=0∘,180∘,360∘,…
Thus, the angles between the vectors that lead to a null vector are 0∘ and 180∘.
The question specifically asks for the angle that results in a null vector. Among the options provided, the angle 180∘ is a valid answer. Therefore, the answer to the question is:
The angle is 180∘.
Similar Questions
Knowledge Check
- Question 1 - Select One
The cross product of two vectors gives zero when the vectors enclose an angle to
A90∘B180∘C45∘D120∘ - Question 2 - Select One
Cross product of vectors obeys
Acommutative lawBassociative lawCdistributive lawDall the above - Question 3 - Select One
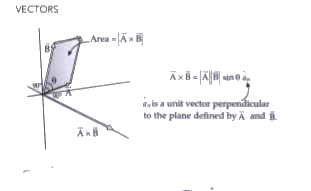
The cross product of two vectors gives a vector perpendicular to the plane containing the vectors.
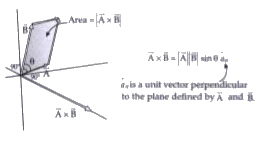
The angle between →a×→b and →b×→a is ___________.A0BπCπ2Dπ4
What is a null vector ?
View SolutionThe cross product of two vectors gives a vector perpendicular to the plane containing the vectors.

ˆi׈j= ___________.View SolutionThe cross product of two vectors gives a vector perpendicular to the plane containing the vectors.
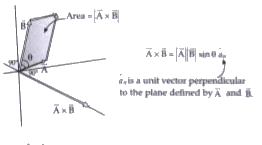
ˆi⋅(ˆj׈k)= __________.View SolutionThe cross product of two vectors gives a vector perpendicular to the plane containing the vectors.
If →a and →b are non-zero vectors, then →a⋅(→a×→b)= _________View SolutionThe vector product of two vector is a vector whose direction is given is given by
View Solution

