A cannon of mass 150 kg shot a cannon ball of 1.5 kg which goes with a velocity of 60 m/s. The cannon will recoil with a speed o
10.5 m/s
6 m/s
0.6 m/s
None of these
The correct Answer is:C
To solve the problem of the cannon recoiling after firing a cannonball, we will use the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a cannon of mass mc=150kg and a cannonball of mass mb=1.5kg that is shot with a velocity vb=60m/s. We need to find the recoil speed vc of the cannon after firing.
Step 2: Apply the Conservation of Momentum
According to the law of conservation of momentum, the total momentum before the event (firing the cannonball) must equal the total momentum after the event.
Initial Momentum:
Since both the cannon and cannonball are at rest before firing, the initial momentum Pinitial is:
Pinitial=0
Final Momentum:
After the cannonball is fired, the momentum of the cannonball and the cannon must equal the initial momentum:
Pfinal=mb⋅vb+mc⋅vc
Where:
- mb is the mass of the cannonball,
- vb is the velocity of the cannonball,
- mc is the mass of the cannon,
- vc is the recoil velocity of the cannon (which we need to find).
Step 3: Set Up the Equation
Since momentum is conserved:
Pinitial=Pfinal
This gives us:
0=mb⋅vb+mc⋅vc
Step 4: Substitute the Known Values
Substituting the known values into the equation:
0=(1.5kg)⋅(60m/s)+(150kg)⋅vc
0=90kg m/s+150kg⋅vc
Step 5: Solve for vc
Rearranging the equation to solve for vc:
150vc=−90
vc=−90150
vc=−0.6m/s
Step 6: Interpret the Result
The negative sign indicates that the cannon recoils in the opposite direction to the cannonball. Thus, the speed of the cannon's recoil is 0.6m/s.
Final Answer
The recoil speed of the cannon is 0.6m/s in the direction opposite to that of the cannonball.
---
We have a cannon of mass mc=150kg and a cannonball of mass mb=1.5kg that is shot with a velocity vb=60m/s. We need to find the recoil speed vc of the cannon after firing.
According to the law of conservation of momentum, the total momentum before the event (firing the cannonball) must equal the total momentum after the event.
Since both the cannon and cannonball are at rest before firing, the initial momentum Pinitial is:
Pinitial=0
After the cannonball is fired, the momentum of the cannonball and the cannon must equal the initial momentum:
Pfinal=mb⋅vb+mc⋅vc
Where:
- mb is the mass of the cannonball,
- vb is the velocity of the cannonball,
- mc is the mass of the cannon,
- vc is the recoil velocity of the cannon (which we need to find).
Since momentum is conserved:
Pinitial=Pfinal
This gives us:
0=mb⋅vb+mc⋅vc
Substituting the known values into the equation:
0=(1.5kg)⋅(60m/s)+(150kg)⋅vc
0=90kg m/s+150kg⋅vc
Rearranging the equation to solve for vc:
150vc=−90
vc=−90150
vc=−0.6m/s
The negative sign indicates that the cannon recoils in the opposite direction to the cannonball. Thus, the speed of the cannon's recoil is 0.6m/s.
The recoil speed of the cannon is 0.6m/s in the direction opposite to that of the cannonball.
Similar Questions
Knowledge Check
- Question 1 - Select One
A canon of mass 150 kg shot a cannon ball of 1.5 kg which goes with a velocity of 60 m/s. the cannon will recoil with a speed of
A10.5 m/sB6 m/sC0.6 m/sDNone of these - Question 2 - Select One
A bullet of mass 50 gram is fired from a 5 kg gun with a velocity of 1 km/s . the speed of recoil of the gun is
A5 m/sB1 m/sC0.5 m/sD10 m/s - Question 3 - Select One
A bullet of mass 50 gram is fired from a 5 kg gun with a velocity of 1 km/s . the speed of recoil of the gun is
A5m/sB1m/sC0.5m/sD10m/s
A cannon of mass 100 kg is kept on a frictionless floor. If a cannon ball of mass 1 kg is fired from it with a speed of 200 m/s. With what velocity the cannon will move?
View SolutionA 10 gram bullet is shot from a 2 kg gun with a velocity of 400 m/s. What is the speed of recoil of the gun ?
View SolutionA bullet of mass 10 g is fired from a gun of mass 1 kg with recoil velocity of gun 5 m/s. The muzzle velocity will be
View SolutionA ball of mass 1kg strink a heavy platform, elastically, moving upwards with a velocity of 5m/s. The speed of the ball just begore the collision is 10m/s downwards. Then the impulse imparted by the platform on the ball is :-
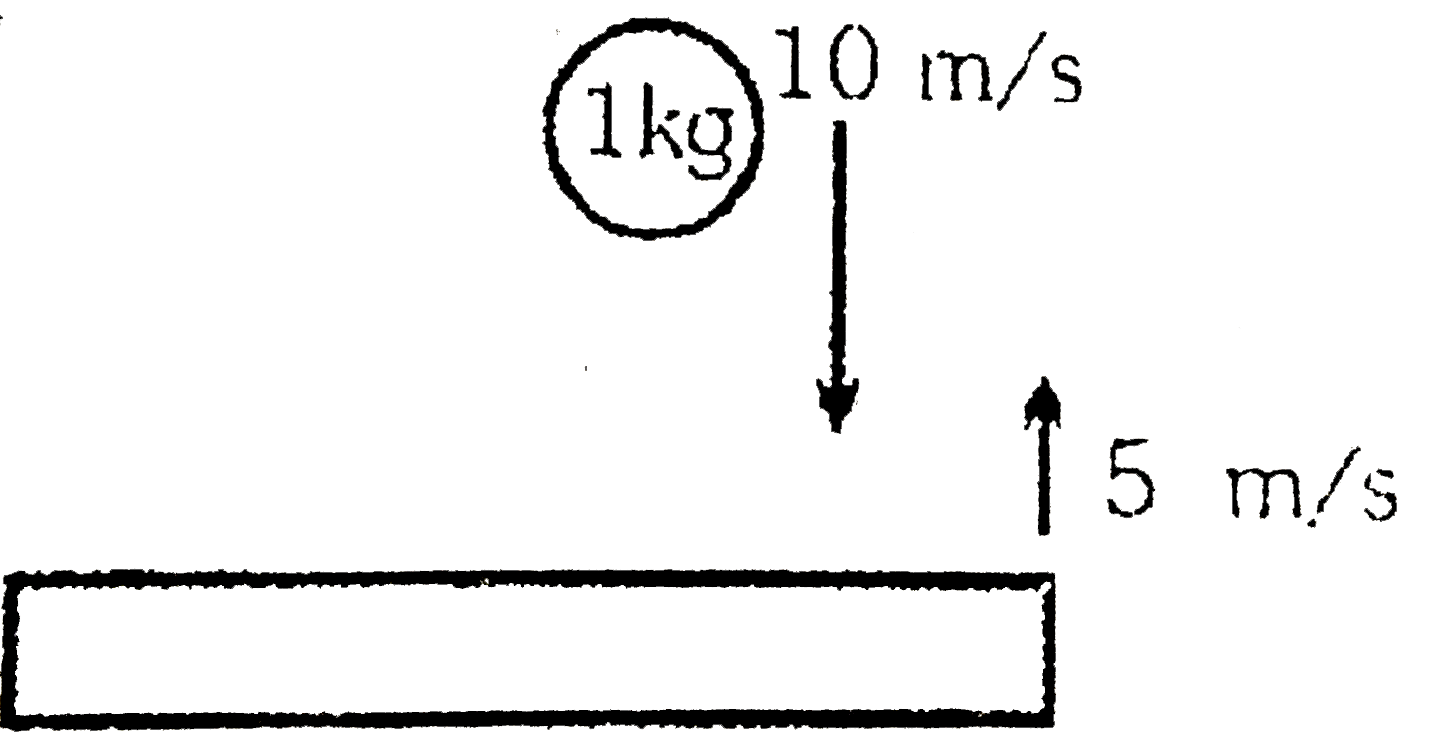 View Solution
View SolutionA field gun of mass 1.5 tonne fires a shell of mass 15kg with a velocity of 150ms−1 . Calculate the velocity of the recoil of the gun
View Solution

