Give an example for complex of the type [Ma2b2c2] where a, b, c are monodentate ligands and give the possible isomers.
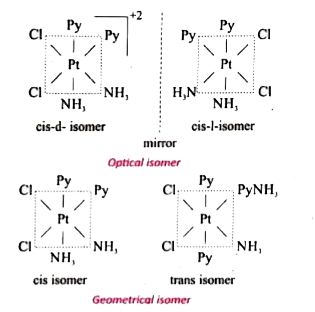
[Ma2b2c2]±n where a,b,c are monodentate ligands. [Pt(py)2(NH3)2Cl2]+2 . It exhibits optical isomerism.
Topper's Solved these Questions
- CO-ORDINATION CHEMISTRY BOOK - PREMIERS PUBLISHERSCHAPTER - CO-ORDINATION CHEMISTRY EXERCISE - Other Important Question & Answer (Choose the correct Answer)
30 Videos
- CO-ORDINATION CHEMISTRY BOOK - PREMIERS PUBLISHERSCHAPTER - CO-ORDINATION CHEMISTRY EXERCISE - Other Important Question & Answer (Answer the following )
165 Videos
- CO-ORDINATION CHEMISTRY BOOK - PREMIERS PUBLISHERSCHAPTER - CO-ORDINATION CHEMISTRY EXERCISE - Textbook Question & Answers (Choose the correct answer )
20 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - PREMIERS PUBLISHERSCHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - OTHER IMPORTANT QUESTIONS& ANSWERS (ANSWER THE FOLLOWING QUESTIONS)
63 Videos
- ELECTRO CHEMISTRYBOOK - PREMIERS PUBLISHERSCHAPTER - ELECTRO CHEMISTRYEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (II. Answer the following questions: )
58 Videos
Similar Questions
The total count of geometrical isomers for a square planar complex [Mabcd]n± is 'x'. The number of geometrical isomers possible for octahedral complex of the type [Ma4b2]n± - is 'y'. Calculate x+y: _______ (a, b, c, d are monodentate ligands).
View SolutionFind the total number of diastereomers of the complex Ma2b2c2 where M is the central metal atom/ion and a, b, c are monodentate achiral ligands.
View Solution
Knowledge Check
A complex MA3X3. Where A and X are unidentate ligands may give
Atwo geometrical isomersBthree geometrical isomersCtwo geometrical isomers which can be resolved into a pair of enantiomersDtwo geometrical isomers one of which can be resolved into a pair of enantiomers .What will be the number of stereoisomers for complex [Ma2b2c2]nt, if its two different monodentate ligends are replaced with one symmetrical bidentate ligand
A3B2C0D1For the square planar complex [M(a) (b) (c ) (d)] (where M = central metal and a, b, c and d are monodentate ligands), the number of possible geometrical isomers are
AoneBtwoCthreeDfour
Find the total number of diastereomers of the complex Ma2b2c2 where M is the central metal atom/ion and a, b, c are monodentate achiral ligands.
View SolutionFor the square planar complex [M(a) (b) (c ) (d)] (where M = central meatal and a, b, c and d are monodentate ligands), the number of possible geometrical isomers are
View SolutionTetrahedral complexes of the types of [MA4] and [MA3B] (where M = central metal, A,B = achiral ligands) are not able to show optical isomerism because
View SolutionThe total number of geometric isomers for Mabcdef are ____________ .
View SolutionIf a complex, Ma4b2 (where M is a central atom and a and b are mondentate ligands ) has trigonal prismatic geometry, the total number of possible geometrical isomers would be :
View Solution
