Derive the equation for acceptance angle and numerical aperture, of optical fiber.
Text Solution
To ensure the critical angle of incidence in core-cladding boundary inside the optical fibre, the light should be incident at a certain angle at the end of the optical fiber while entering into it. This angle is called acceptance angle.
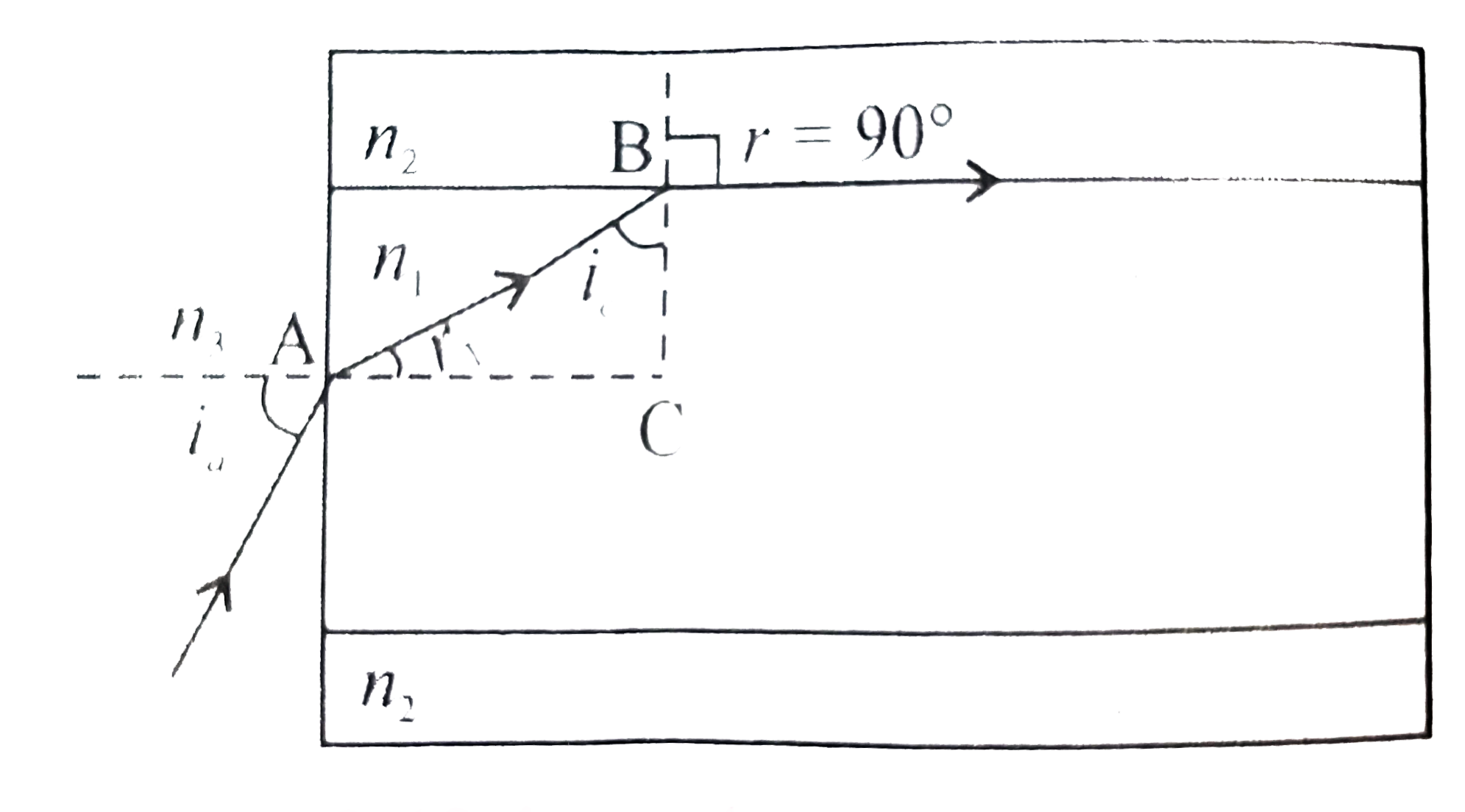
Let the refractive indices of the core n1 cladding n2 and the outer medium n3. Assume the light is incident at an angle called acceptance angle ia at the outer medium and core boundary at A. By Snell.s law of refraction at A,
n3sinia=n1sinra.......(1)
To get total internal reflection inside optical fibre, the angle of incidence at the core-cladding interface at B should be atleast critical angle ic By Snell.s law of refraction at B
n1sinic=n2sin90∘
n1sinic=n2
sinic=n2n1.......(2)
In ABC, ic+90∘+ra=180∘
ic=90∘−ra
sin(90∘−ra)=n2n1
cosra=n2n1
sinra=√1−cos2ra=
⎷n21−n22n21
n1sinra=n1√n21−n22n1=√n21−n22
From (1) n3sinia=√n21−n22....(4)
ia=sin−1⎛⎜⎝
⎷n21−n22n23⎞⎟⎠
If the outer medium is air, then n3=1
The acceptance angle ia=sin−1(√n21−n22)
The term n3sinia is called numerical aperature NA of optical fibre.
NA=n3sinia=√n21−n22
If the outer medium is air then n3=1. Then NA=n3sinia=√n21−n22
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
Which is true for optical fibers?
ACore has higher refractive index than claddingBCore has less refractive index than claddingCBoth have same refractive indexDNone of these - Question 2 - Select One
What should be the maximum acceptance angle at the air–core interface of an optical fibre if n1 and n2 are the refractive indices of the core and the cladding, respectively
Asin−1(n2/n1)Bsin−1√n21−n22C[tan−1.n2n1]D[tan−1.n1n2]] - Question 3 - Select One
In optical fibre, refractive index of inner part is 1.68 and refractive index of outer part is 1.44. The numerical aperture of the fibre is
A0.5653B0.6553C0.7653D0.8753
What should be the maximum acceptance angle at the aircore interface of an optical fibre if 1 n and 2 n are the refractive indices of the core and the cladding, respectively
View SolutionExplain the working of optical fibers.
View SolutionIn optical fibre, refractive index of inner part is 1.68 and refractive index of outer part is 1.44. The numerical aperture of the fibre is
View SolutionIn optical fibre, refractive index of inner part is 1.68 and refractive index of outer part is 1.44. The numerical aperture of the fibre is
View SolutionCalculate the limit of resolution of microscope, if the numerical aperture of microscope is 0.12, and the wavelength of light used is 600 nm
View Solution
