Prove laws of refraction using Huygens' principle.
Text Solution
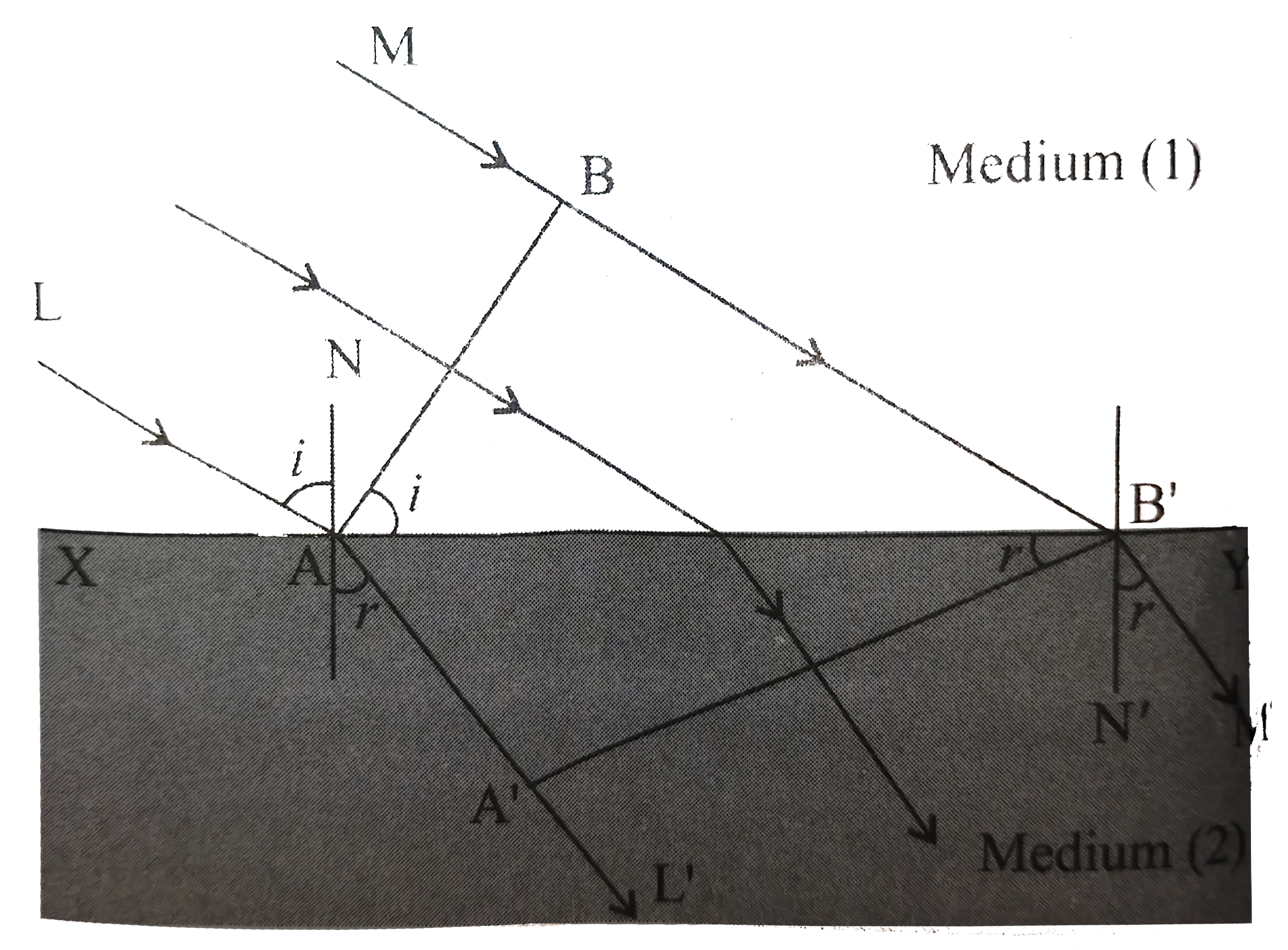
Let us consider a parallel beam of light is incident on a refracting plane surface XY such as a glass surface as shown in fig. The incident wavefront AB is in rarer medium and the refracted wavefront A.B. is in the denser medium (2). These wavefronts are perpendicular to the incident rays L, M and refracted rays L., M. respectively. By the time the point A of the incident wavefront touches the refracting surface, the point B is yet to travel a distance BB. to touch the refracting surface at B..
When the point B falls on the refracting surface at B., the point A would have reached A. in the other medium. This is applicable to all points on the wave front. Thus, the refracted wave front A. B emanates as a plane wavefront. The two normals N and N. are considered at the points where the rays L and M falls on the refracting surface. As refraction happens from rarer medium 1 to the denser medium 2, the speed of the light is v1andv2, before and after the refraction and v1 is greater than v2. But, the time taken t for the ray to travel from B to B. is the same as the time taken for the ray to travel from A to A.
t=BB.v1=∀.v1
BB.∀.=v1v2
(i) The incident rays, the refracted rays and the normal are in the same plane.
(ii) Angle of incidence
∠i=∠NAL=90∘−∠NAB=∠BAB.
Angle of refraction
r=∠N.B.M.=90∘−∠N.B.A.=∠A.B.A
For the two right angle triangles ΔABB.andΔB.A.A
sinisinr=BB./AB.∀./AB.=BB.∀.=v1v2=c/v2c/v1
Here, c is the speed of light in vacuum. The ratio c/v is constant, called refractive index of the medium. The refractive index of the medium (1) is c/v1=n1 and that of medium (2) is c/v2=n2
sinisinr=n2n1
In product form, n1sini=n2sinr
Hence, the laws of refraction is proved.
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One or More
One can use Huygen's principle to
Aexplain law of reflectionBexplain Snell's lawCfind new location of wavefrontDcalculate speed of light in vacuum
Huygen's principle states that
View SolutionDefine the term wavefront. Using Huygens' wave theory, verify the laws of reflection.
View SolutionDeduce Snell's Law of refraction for a plane wave using Huygen's principle.
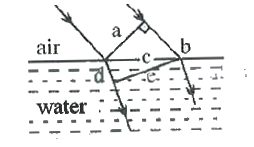
View SolutionFigure shown plane waves refracted for air to water using Huygen.s principle a,b,c,d ,e are lengths on the diagram . The ratio of refractive index of water w.r.t air is
 View Solution
View SolutionHuygen.s principle is used
View SolutionState Huygen's principle for the propagation of light and prove the laws of refraction of light on its basis.
View SolutionDefine a wavefront. Using Huygen's principle, verifyi the laws of reflection at a plane surface.
View Solution

