Establish the relation $\frac{1}{u} + \frac{1}{v} = \frac{1}{f}$ for a convex mirror.

Text Solution

Verified by Experts

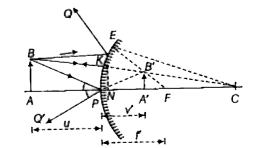
Now, triangles A. B. F. and ENF are similar. Therefore,
$\frac{A . B .}{N E} = \frac{A . F}{N F}$
As aperture of the concave mirror is small, NF=PF. Also, NE = AB
$\frac{A . B .}{A B} = \frac{A . F}{P F}$
Since, the distances are to be measured from pole of the mirror, we have
$A . F = P F - P A .$
$∴ \frac{A . B .}{A B} = \frac{P F - P A .}{P F} ... (i)$
Also, triangles ABP and A.B.P are similar.
Therefore, $\frac{A . B .}{A B} = \frac{P A .}{P A} ... . (i i)$
From Eqs. (i) and (ii), we have
$\frac{P F - P A .}{P F} = \frac{P A .}{P A} ... . (i i i)$
Applying sign conventions, we have
PA= -u (distance of object is measured against the incident light)
PA. = +v ( distance of image is measured along the incident light)
PF = + f ( focal length of convex mirror is measured along the incident light)
Substituting for PA, PA. and PF in Eq (iii), we have
$\frac{+ f - (+ v)}{+ f} = \frac{+ v}{- u} or \frac{f - v}{f} = \frac{- v}{u}$
or $1 - \frac{v}{f} = \frac{- v}{u} or \frac{1}{v} - \frac{1}{f} = \frac{- 1}{u}$
$∴ \frac{1}{v} + \frac{1}{u} = \frac{1}{f}$

Updated on:21/07/2023

The graph between $\frac{1}{v}$ and $\frac{1}{u}$ for a concave mirror looks like.
A
B
C
D
What is f in mirror formula $\frac{1}{u} + \frac{1}{v} = \frac{1}{f}$ ?
Adistance of object
Bdistance of image
Cfocal length
DNone.
By Plotting $\frac{1}{v}$ verus $\frac{1}{u}$ focal length of a convex mirror can be found .
ANo as it forms a virtual image
BYes only if scale is large
CYes only if scale is small
DYes only if aperture is small