Question

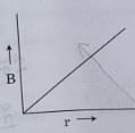
A thick current carrying cable of radius 'R' carries current 'I' uniformly distributed across its crosssection. The variation of magnetic field B(r) due to cable with distance 'r' from the axis of the cable is represented by.

Options

A.
B.
C.
D.

Explanation

To solve the problem of the variation of the magnetic field $$B\left(r\right)$$ due to a thick current-carrying cable of radius $$R$$ that carries a current $$I$$ uniformly distributed across its cross-section, we can use Ampère's Law. Here’s a step-by-step solution:

Step 1: Understand the Configuration
We have a thick cylindrical cable of radius \( R \) carrying a current \( I \) uniformly distributed across its cross-section. We need to analyze the magnetic field \( B(r) \) at a distance \( r \) from the axis of the cable.

Step 2: Apply Ampère's Law
Ampère's Law states that:
\( \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{\text{enc}} \)
where \( I_{\text{enc}} \) is the current enclosed by the Amperian loop.

Step 3: Case 1 - Inside the Cable (\( r < R \))
For points inside the cable (where \( r < R \)):
- The current density \( J \) is given by:
\( J = \frac{I}{\pi R^2} \)
- The enclosed current \( I_{\text{enc}} \) for a radius \( r \) is:
\( I_{\text{enc}} = J \cdot A = J \cdot \pi r^2 = \frac{I}{\pi R^2} \cdot \pi r^2 = I \frac{r^2}{R^2} \)
- Now, applying Ampère's Law:
\( B(2\pi r) = \mu_0 I_{\text{enc}} \implies B(2\pi r) = \mu_0 \left(I \frac{r^2}{R^2}\right) \)
- Therefore, the magnetic field inside the cable is:
\( B(r) = \frac{\mu_0 I r}{2 \pi R^2} \)

Step 4: Case 2 - Outside the Cable (\( r \geq R \))
For points outside the cable (where \( r \geq R \)):
- The entire current \( I \) is enclosed:
\( I_{\text{enc}} = I \)
- Applying Ampère's Law:
\( B(2\pi r) = \mu_0 I \implies B(2\pi r) = \mu_0 I \)
- Therefore, the magnetic field outside the cable is:
\( B(r) = \frac{\mu_0 I}{2 \pi r} \)

Step 5: Summary of Results
- For \( r < R \):
\( B(r) = \frac{\mu_0 I r}{2 \pi R^2} \)
- For \( r \geq R \):
\( B(r) = \frac{\mu_0 I}{2 \pi r} \)

Step 6: Graphical Representation
- The magnetic field \( B(r) \) increases linearly with \( r \) for \( r < R \) and decreases hyperbolically for \( r \geq R \).

Conclusion
The variation of the magnetic field \( B(r) \) with distance \( r \) from the axis of the cable can be represented as:
- A linear increase for \( r < R \)
- A hyperbolic decrease for \( r \geq R \)