In the exponential growth equation
The base of natural logarithms
The base of geometric logarithms
The base of number logarithms
The base of exponential logarithms
To solve the question regarding the base of the exponential growth equation, we can follow these steps:
1. Understanding the Exponential Growth Equation:
The exponential growth of a population can be represented mathematically. The general form of the equation is:
dNdt=RmaxN
where:
- dNdt is the change in population over time,
- Rmax is the maximum intrinsic growth rate (biotic potential),
- N is the population size.
Hint: This equation describes how populations grow under ideal conditions.
2. Integrating the Equation:
To find the population at any time t, we can integrate the equation. The solution to this differential equation is:
N(t)=N0eRmaxt
where:
- N(t) is the population at time t,
- N0 is the initial population size at time t=0,
- e is the base of the natural logarithm.
Hint: The function eRmaxt shows how the population increases exponentially over time.
3. Identifying the Base:
In the equation N(t)=N0eRmaxt, the base of the exponential function is e. This is a fundamental constant approximately equal to 2.71828, and it is the base of natural logarithms.
Hint: Remember that e is a crucial mathematical constant used in continuous growth models.
4. Conclusion:
Therefore, the base of the exponential growth equation is e, which corresponds to the natural logarithm.
Hint: When asked about the base in exponential growth, always think of e as it is widely used in biological growth models.
Final Answer:
The base of the exponential growth equation is e (the natural logarithm base).
The exponential growth of a population can be represented mathematically. The general form of the equation is:
dNdt=RmaxN
where:
- dNdt is the change in population over time,
- Rmax is the maximum intrinsic growth rate (biotic potential),
- N is the population size.
To find the population at any time t, we can integrate the equation. The solution to this differential equation is:
N(t)=N0eRmaxt
where:
- N(t) is the population at time t,
- N0 is the initial population size at time t=0,
- e is the base of the natural logarithm.
In the equation N(t)=N0eRmaxt, the base of the exponential function is e. This is a fundamental constant approximately equal to 2.71828, and it is the base of natural logarithms.
Therefore, the base of the exponential growth equation is e, which corresponds to the natural logarithm.
The base of the exponential growth equation is e (the natural logarithm base).
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the following graph, which of the expressions of the exponential growth equation should be increased in order for curve 1 to become more like curve 2?
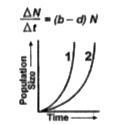 AN−BdCbD(b-d)
AN−BdCbD(b-d)The integral form of the exponential growth equation as Nt=N0ert
A. population density after time t
B. population density at time zero
C. intrinsic rate of natural increase
D. the base of natural logarithms (2.71828)
Identify A,B,C and D fromt eh given equation.AA-r,B-e,C-No,D-NtBA−Nt,B−N0,C−r,D−eCA−N0,B−Nt,C−r,D−eDA−N0,B−Nt,C−e,D−rThe integral form of exponential growth equation will be
AN0=NtertBNt−No=ertCNt=NoertDNtNo=1ert
