Study the given information carefully and answer the following questions.
There was a football tournament of three teams i.e. A, B and C in which each team played 2 matches. Score pattern of the tournament is:
• A team gets 2 points for scoring a goal against the opponent team.
• A team gets 3 points for scoring a goal against the opponent team from the outside area.
• There is a penalty of 1 point if a team concedes a goal.
• Only three players from each team scored the goals.
A – B Match: B is the winner of this game. Total points scored by B in this match is 4 . Also, team A scored 2 goals and none of the players scored the goal from the outside area.
A – C Match: C scored 0 points in the match. Only one player from team A scored a goal from outside area. A scored 4 points in this match.
B – C Match: B gets 6 points from match. Team C scored 1 goal more than Team B. One player from team B scored a goal from outside area but none from team C.
The given 3 teams are ranked on the basis of total marks in such a way that the highest scoring team is ranked 1, the second highest scoring team is ranked 2 and the least scoring team is ranked 3. Rank 3 got a total of Rs. 60,000 as prize money. If the ratio of the prize money of the rank 1, rank 2 and rank 3 team is 8 : 5 : 3, which of the following combinations of team and prize money is correct?
A, Rs. 1,00,000
C, Rs. 1,60,000
B, Rs. 1,60,000
C, Rs. 1,20,000
The correct Answer is:C
To solve the problem step-by-step, we need to analyze the information given about the football tournament involving teams A, B, and C.
Step 1: Analyze the A-B Match
- B wins the match against A.
- Total points scored by B in this match = 4.
- Team A scored 2 goals and none from outside.
Since A scored 2 goals:
- Points for A = 2 goals × 2 points/goal = 4 points.
- B must have scored 3 goals (since A conceded 2 goals, B gets points for those).
- Points for B = 3 goals × 2 points/goal - 1 point (penalty for conceding) = 6 - 1 = 5 points.
However, since B scored a total of 4 points, it can be concluded that:
- B scored 2 goals (2 points each) and 1 goal from outside (3 points).
- Therefore, B's total points = 2 goals × 2 points + 3 points (outside goal) - 1 point (penalty) = 4 points.
Step 2: Analyze the A-C Match
- C scored 0 points in this match.
- A scored 4 points.
- Only one player from team A scored a goal from outside.
Since A scored 4 points:
- Points for A = 3 points (for the outside goal) + 2 points (for one inside goal) = 5 points.
- Since C scored 0 points, A must have scored 2 goals (1 from outside and 1 from inside).
Step 3: Analyze the B-C Match
- B gets 6 points from this match.
- Team C scored 1 goal more than Team B.
- One player from team B scored a goal from outside, and none from team C.
Let’s denote the goals scored by B as x. Then C scored x + 1 goals.
- Points for B = 3 points (for the outside goal) + (x - 1) × 2 points (for the inside goals).
Since B scored 6 points:
- 3 + 2(x - 1) = 6
- 2(x - 1) = 3
- x - 1 = 1.5 (not possible, x must be an integer).
Let’s assume B scored 2 goals:
- Points for B = 3 (outside goal) + 2 (inside goal) - 1 (penalty for conceding) = 4 points.
If B scored 2 goals, then C scored 3 goals (1 more than B):
- Points for C = 3 goals × 2 points = 6 points.
Step 4: Calculate Total Points for Each Team
- Team A:
- A-B Match: 4 points
- A-C Match: 4 points
- Total for A = 4 + 4 = 8 points.
- Team B:
- A-B Match: 4 points
- B-C Match: 6 points
- Total for B = 4 + 6 = 10 points.
- Team C:
- A-C Match: 0 points
- B-C Match: 6 points
- Total for C = 0 + 6 = 6 points.
Step 5: Determine Rankings
- Team B: 10 points (Rank 1)
- Team A: 8 points (Rank 2)
- Team C: 6 points (Rank 3)
Step 6: Prize Money Distribution
- Rank 3 (Team C) gets Rs. 60,000.
- The ratio of prize money for Rank 1, Rank 2, and Rank 3 is 8:5:3.
Let the prize money for Rank 1 = 8x, Rank 2 = 5x, and Rank 3 = 3x.
- 3x = 60,000 → x = 20,000.
- Therefore, prize money for:
- Rank 1 = 8x = 160,000
- Rank 2 = 5x = 100,000
- Rank 3 = 3x = 60,000.
Final Answer
The correct combination of team and prize money is:
- Team B: Rs. 160,000
- Team A: Rs. 100,000
- Team C: Rs. 60,000
- B wins the match against A.
- Total points scored by B in this match = 4.
- Team A scored 2 goals and none from outside.
Since A scored 2 goals:
- Points for A = 2 goals × 2 points/goal = 4 points.
- B must have scored 3 goals (since A conceded 2 goals, B gets points for those).
- Points for B = 3 goals × 2 points/goal - 1 point (penalty for conceding) = 6 - 1 = 5 points.
However, since B scored a total of 4 points, it can be concluded that:
- B scored 2 goals (2 points each) and 1 goal from outside (3 points).
- Therefore, B's total points = 2 goals × 2 points + 3 points (outside goal) - 1 point (penalty) = 4 points.
- C scored 0 points in this match.
- A scored 4 points.
- Only one player from team A scored a goal from outside.
Since A scored 4 points:
- Points for A = 3 points (for the outside goal) + 2 points (for one inside goal) = 5 points.
- Since C scored 0 points, A must have scored 2 goals (1 from outside and 1 from inside).
- B gets 6 points from this match.
- Team C scored 1 goal more than Team B.
- One player from team B scored a goal from outside, and none from team C.
Let’s denote the goals scored by B as x. Then C scored x + 1 goals.
- Points for B = 3 points (for the outside goal) + (x - 1) × 2 points (for the inside goals).
Since B scored 6 points:
- 3 + 2(x - 1) = 6
- 2(x - 1) = 3
- x - 1 = 1.5 (not possible, x must be an integer).
- Points for B = 3 (outside goal) + 2 (inside goal) - 1 (penalty for conceding) = 4 points.
If B scored 2 goals, then C scored 3 goals (1 more than B):
- Points for C = 3 goals × 2 points = 6 points.
- Team A:
- A-B Match: 4 points
- A-C Match: 4 points
- Total for A = 4 + 4 = 8 points.
- Team B:
- A-B Match: 4 points
- B-C Match: 6 points
- Total for B = 4 + 6 = 10 points.
- Team C:
- A-C Match: 0 points
- B-C Match: 6 points
- Total for C = 0 + 6 = 6 points.
- Team B: 10 points (Rank 1)
- Team A: 8 points (Rank 2)
- Team C: 6 points (Rank 3)
- Rank 3 (Team C) gets Rs. 60,000.
- The ratio of prize money for Rank 1, Rank 2, and Rank 3 is 8:5:3.
Let the prize money for Rank 1 = 8x, Rank 2 = 5x, and Rank 3 = 3x.
- 3x = 60,000 → x = 20,000.
- Therefore, prize money for:
- Rank 1 = 8x = 160,000
- Rank 2 = 5x = 100,000
- Rank 3 = 3x = 60,000.
The correct combination of team and prize money is:
- Team B: Rs. 160,000
- Team A: Rs. 100,000
- Team C: Rs. 60,000
Similar Questions
The following is the record of goals scored by team A in a football season.For the team b mean number of goals scored per match was 2 with a standard deviation of 1.25 goals. Find which team may be consider more consistent using coefficient of variation.
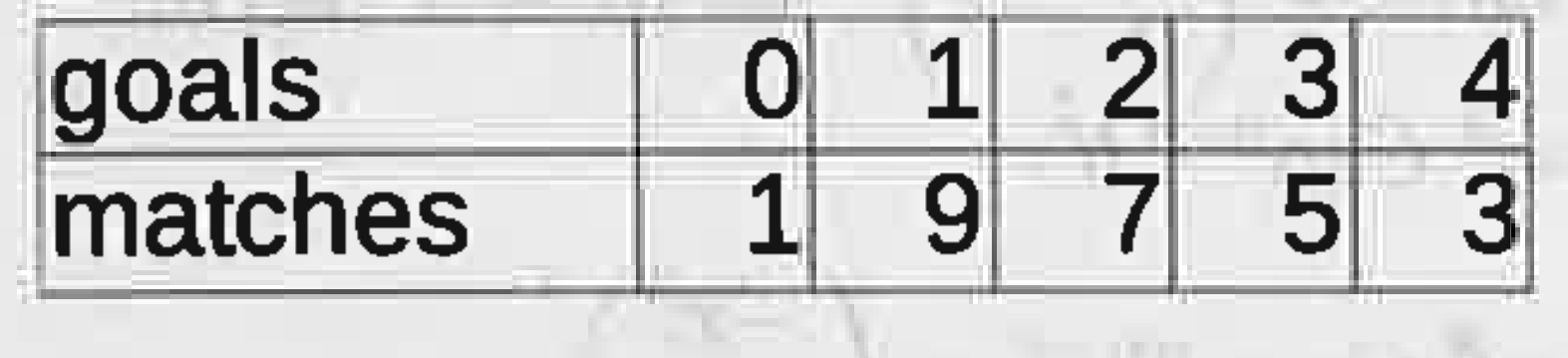
View SolutionThe following is the record of goals scored by team A in a football session

View SolutionThe following is the rècord of goals scored by team '(A)' in a football session.

View SolutionIn a tournament with five teams, each team plays against every other team exctly once. Each game is won by one of the playing teams and the winning team scores one point, while the losing team scores zero. Which of the following is NOT necessarily true?
View SolutionTwenty teams take part in a football tournament. Each team has to play every other team. How many games would be played in the tournament?
View SolutionThe line chart given below represents the runs scored by Kohli and Sharma against 5 teams.
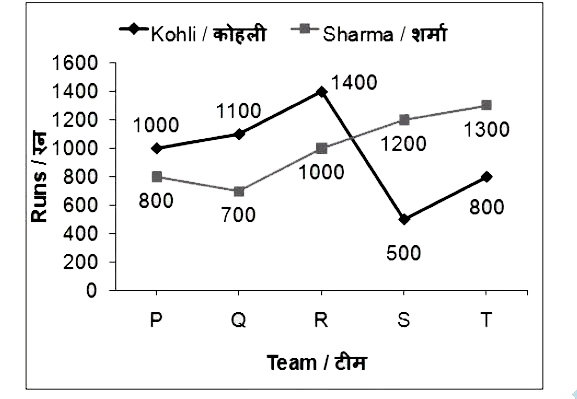
Total runs scored by Sharma against 5 teams is what percent of total runs scored by Kohli against 5 teams?
View SolutionStudy the given information carefully and answer the following questions. There was a football tournament of three teams i.e. A, B and C in which each team played 2 matches. Score pattern of the tournament is: • A team gets 2 points for scoring a goal against the opponent team. • A team gets 3 points for scoring a goal against the opponent team from the outside area. • There is a penalty of 1 point if a team concedes a goal. • Only three players from each team scored the goals. A – B Match: B is the winner of this game. Total points scored by B in this match is 4 . Also, team A scored 2 goals and none of the players scored the goal from the outside area. A – C Match: C scored 0 points in the match. Only one player from team A scored a goal from outside area. A scored 4 points in this match. B – C Match: B gets 6 points from match. Team C scored 1 goal more than Team B. One player from team B scored a goal from outside area but none from team C. What is the maximum possible sum of the total number of goals scored by those players of all three teams, who score more than one goal in a tournament?
View Solution
