A nail is located at a certain distance vertically below the point of suspension of a simple pendulum .the pendulum bob is released from a position where the string makes an angle of $60^{\circ}$ with the vertical .Calculate the distance of nail from the point of suspension such that bob will just perform revolution with the nail as centre . Assume the length of the pendulum to be one metre .

Text Solution

Verified by Experts

If r is the radius of the loop about the nail , for just completing the revolution
$v_{L} = \sqrt{5 g r}$ ---------(i)

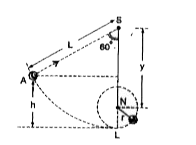
Now , this $v_{L}$ is provided by conversion of potential energy of the bob into energy in moving from A to l , so by conversation of mechanical energy between A and L .
$\frac{1}{2} m v_{L}^{2} = m g L (1 - cos θ)$ ---------(ii)
[ as h = L $(1 - cos θ)$ ]
Now , substituting the value of $v_{L}$ from Eqn ,(i) in (ii) $5 g r = 2 g L (1 - cos θ)$
or $r = \frac{2}{5} \times 1 [1 - \frac{1}{2}] = \frac{1}{5} = 0.2$ m
Now , substituting the value of $v_{L}$ from Eqn ,(i) in (ii) $5 g r = 2 g L (1 - cos θ)$
or $r = \frac{2}{5} \times 1 [1 - \frac{1}{2}] = \frac{1}{5} = 0.2$ m
$L - r = 1 - 0.2 = 0.8$ m

Updated on:21/07/2023

A nail is fixed at a point $P$ vertically below the point of suspension 'O' of simple pendulum of length $1 m$ . The bob is released when the string of pendulum makes an angle $30^{\circ}$ with horiozontal. The bob reaches lowest point and then describes vertical circle whose centre coincides with $P$ . The least distance of $P$ from $O$ is
A $0.4 m$
B $0.5 m$
C $0.6 m$
D $0.8 m$
The distance between the points of suspension and centre of oscillation for a compound pendulum is :
A $\frac{k^{2} - l^{2}}{2}$
B $\frac{k^{2} + l^{2}}{l}$
C $\frac{k^{2} + l^{2}}{2 l}$
D $k + \frac{l^{2}}{k}$
A simple pendulum of length I and mass (bob) m is suspended vertically. The string makes an angle $θ$ with the vertical. The restoring force acting on the pendulum is
A $m g tan θ$
B $- m g sin θ$
C $m g sin θ$
D $- m g cos θ$