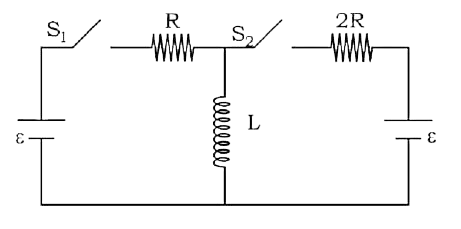
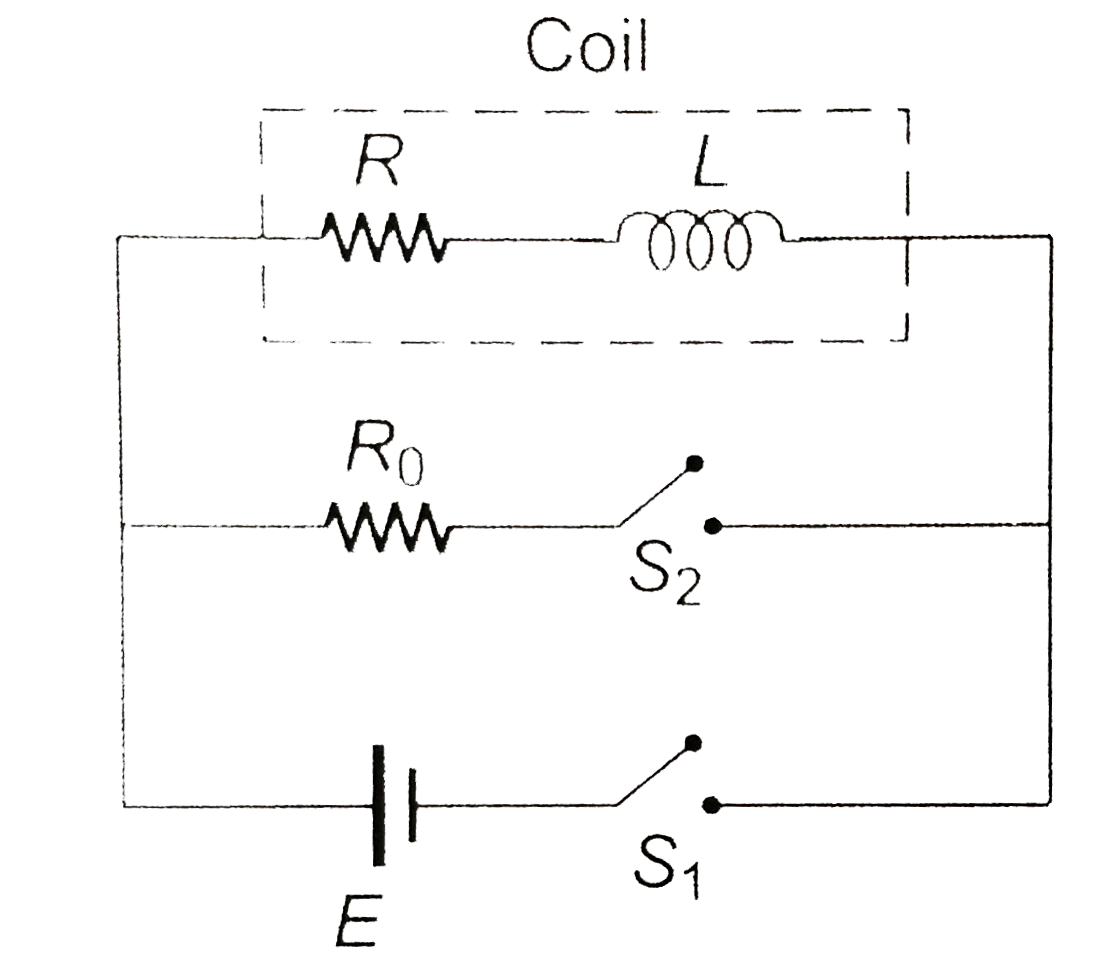
In the circuit chown in Fig, S1 and S2 are switches. S2 remains closed for a long time and S1 is opened. Now S1 is also closed. Just after S1 is closed, the potential difference (V) across R will be
ε
ε2
ε3
ε4
The correct Answer is:C
Before closing S1, current in the inductor is i=ε2R. Just after closing S1, current in inductor will remain same, other currents are as shown.

For left loop ε=i1R+L(didt) . . . (1)
For right loop ε=i22R+L(didt) . .. (2)
Eq. (1)×2+Eq.(2)
2∈=2i1R+2L(didt)
∈=2i2R+Ldidt⇒
3∈=2(i1+i2)R+3Ldidt
3∈=2iR+3Ldidt, But i=∈2R
3∈=2∈2RR+3Ldidt
2∈=3Ldidt ∴didt=2∈3L
i1+i2=i . . . . . (3)
didt=2ε3L, p.d. across R :VR=i1R=ε−L(2ε3L)=ε3
Similar Questions
In the circuits shows in S1 and S2 are switches. S2 remains closed for a long time and S1 is opened. Now S1 is also closed. Just after S1 is closed, find the potential difference (V) across R and di/dt (with sign) in L.

View SolutionIn the circuits shows in S1 and S2 are switches. S2 remains closed for a long time and S1 is opened. Now S1 is also closed. Just after S1 is closed, find the potential difference (V) across R and di/dt (with sign) in L.

View Solution
Knowledge Check
In the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
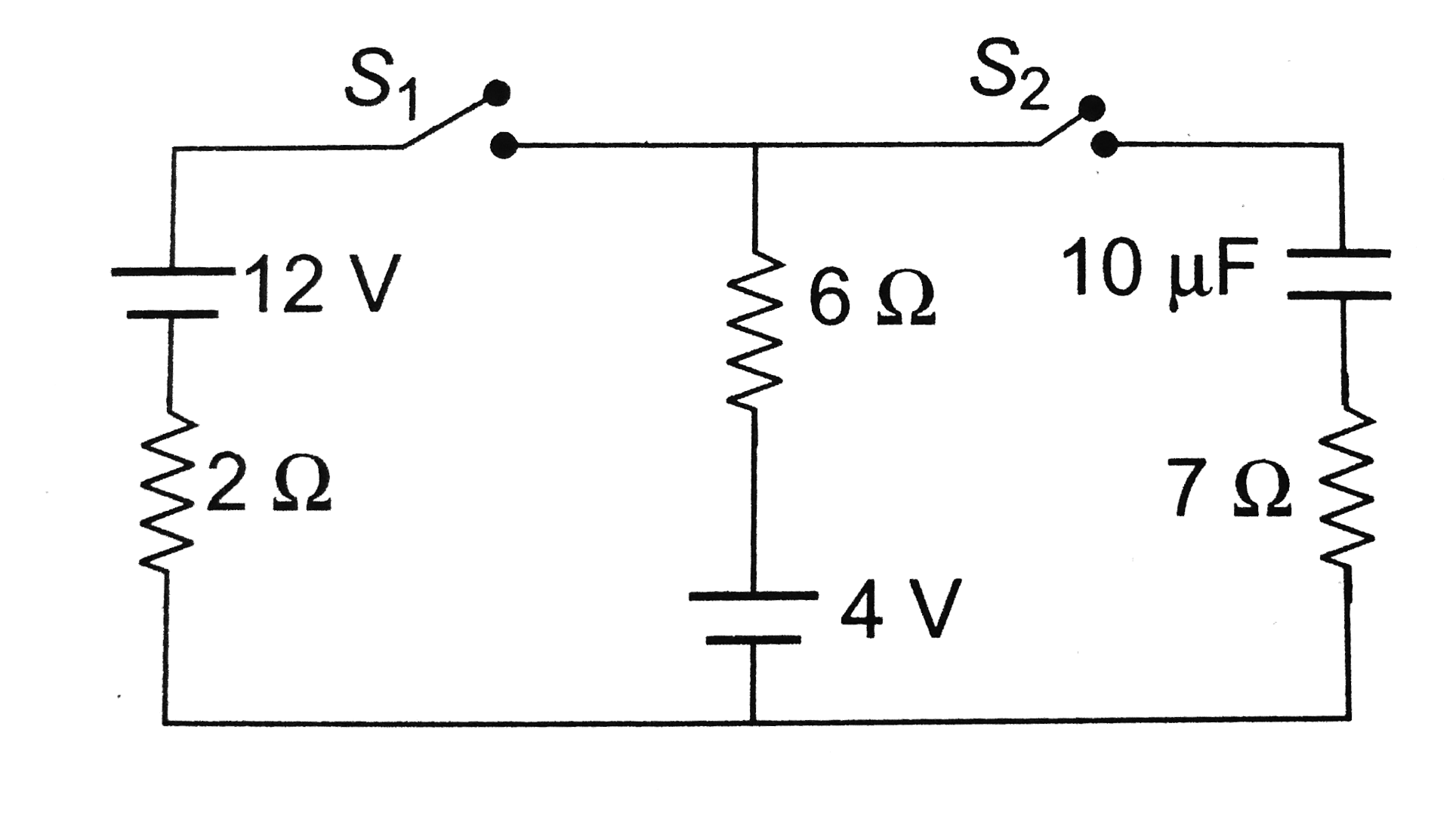 Ais 100μCBincreases to 200μC if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same areaCboth (a) and (b) aboveDcharge on the capacitor remains unchanged if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same area.
Ais 100μCBincreases to 200μC if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same areaCboth (a) and (b) aboveDcharge on the capacitor remains unchanged if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same area.In Fig. switch S is closed for a long time. At t=0, if it is opened, then
 Atotal heat produced in resistor R after opening the switch is 12LεR2Btotal heat produced in resistor R1 after opening the switch is 12Lε2R2(R1R1+R2)Cheat produced in resistor R1 after opening the switch is 12R2Lε2(R1+R2)R2Dno heat will be produced in R1
Atotal heat produced in resistor R after opening the switch is 12LεR2Btotal heat produced in resistor R1 after opening the switch is 12Lε2R2(R1R1+R2)Cheat produced in resistor R1 after opening the switch is 12R2Lε2(R1+R2)R2Dno heat will be produced in R1
In the given circuit S1 and S2
are switches. S2 is closed for
a long time and S1 remains
Open. Now S1 is also closed. Here
R=10Ω,L=1 mH and
ε=3V.Letdidt is the
magnitude of rate of change of
current (in"A/s"). Just after S1
is Closed. The value for the
inductor L is
didt=x×103A/s. Then find x.
View SolutionIn the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
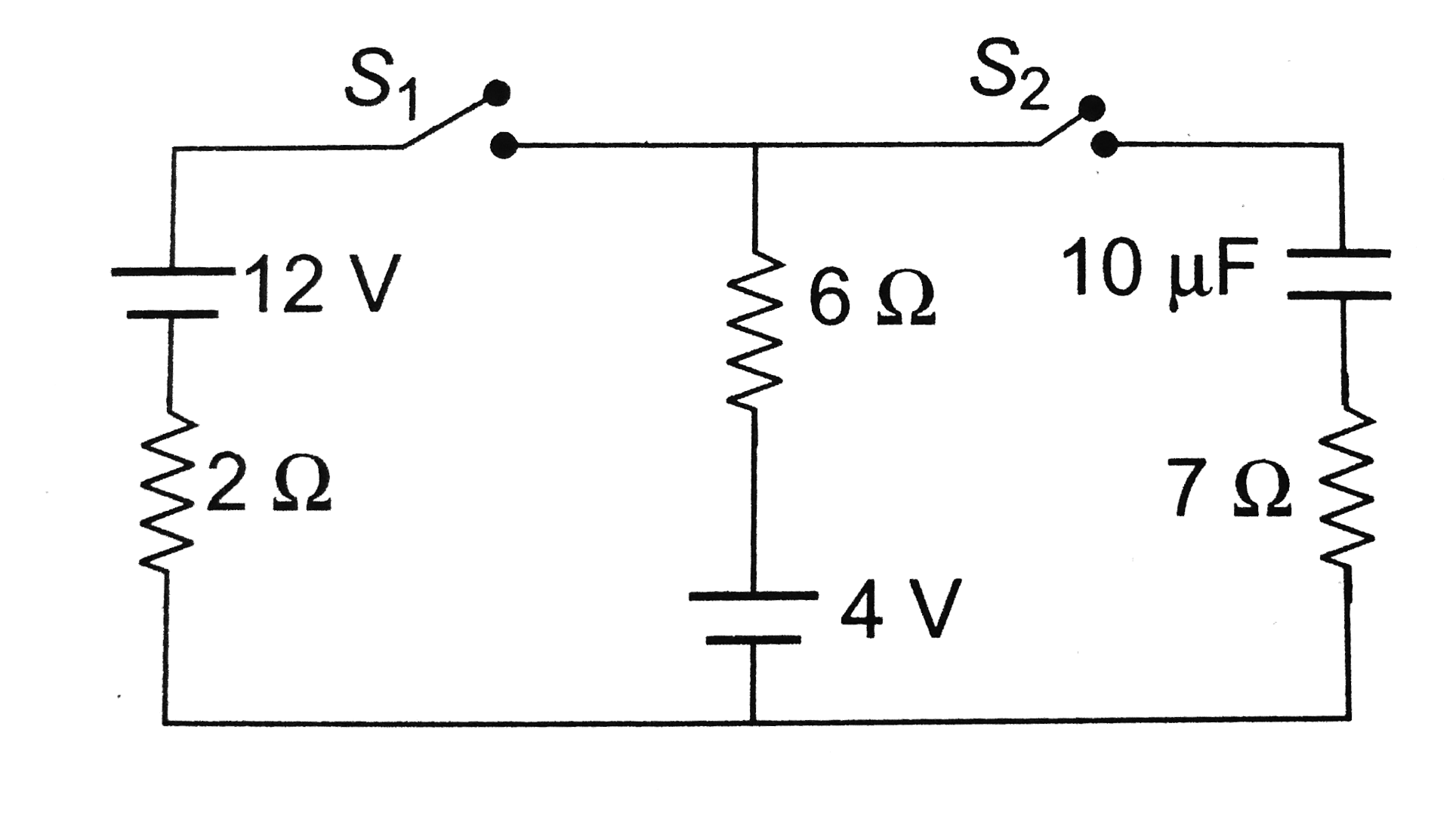
View SolutionIn a circuit S1 remains closed for a long time and S2 remain open. Now S2 is closed and S1 is opened. Find out the di/dt in the right loop just after the moment.

View SolutionIn a circuit S1 remains closed for a long time and S2 remain open. Now S2 is closed and S1 is opened. Find out the di/dt in the right loop just after the moment.

View SolutionIn a circuit S1 remains closed for a long time and S2 remain open. Now S2 is closed and S1 is opened. Find out the di/dt in the right loop just after the moment.

View SolutionInitally switch S1 is closed, after a long time, S1 is opened and S2 is closed. Find the heat produced in coil after long time.
View Solution
