Find the co-ordinates of the point R, which divides the join of P (0, 0, 0) and Q (4, -1, -2) in the ratio 1 : 2 externally and verify that P is the mid-point of [RQ].Solution in Punjabi
Step by step video & image solution for Find the co-ordinates of the point R, which divides the join of P (0, 0, 0) and Q (4, -1, -2) in the ratio 1 : 2 externally and verify that P is the mid-point of [RQ]. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE86videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
- BOOK - MODERN PUBLICATIONCHAPTER - INFINITE SERIESEXERCISE - EXAMPLE10videos
INFINITE SERIES
- BOOK - MODERN PUBLICATIONCHAPTER - LIMITS AND DERIVATIVESEXERCISE - EXERCISE334videos
LIMITS AND DERIVATIVES
Similar Questions
A point is on x-axis. What are its y-co-ordinate and z-co-ordinate ?
03:15View SolutionExpand (1−x2)−1/2 when | x | < 2.
03:15View SolutionEvaluate the following limit if they exist :
limx→24.02:04View SolutionFind the coordinates of the point R which divides PQ externally in the ratio 2:1 and verify that Q is the mid point of PR.
03:02View SolutionFind the coordinates of the point R which divides the join of P(0,0,0)andQ(4,−1,−2) in the ratio 1:2 externally and verify that P is the mid point of RQ.
04:11View SolutionFind the co-ordinates of a point which divides the line segment joining P(5, 4, 2) and Q(-1, -2, 4) in the ratio 2 : 3.
04:29View SolutionFind the co-ordinates of a point which divides the line segment joining the points (3, 0) and (0, 2) in the ratio 2 : 1 externally.
A. (3,4)
B. (−3,4)
C. (3,−4)
D.(−3,−4)03:05View SolutionLet P be a point on x2=4y. The segment joining A(0,−1) and P is divided by point Q in the ratio 1:2, then locus of point Q is
04:29View Solutionबिन्दु R के निर्देशांक निकालें जो P (0, 0, 0) तथा Q (4, -1, -2) को मिलाने वाली रेखाखण्ड को 1 : 2 के अनुपात में बहिर्विभजित करता है। सत्यापित करें कि P, RQ का मध्य बिन्दु है।
05:47View SolutionLet P and Q be any two points. Find the coordinates of the point R which divides PQ externally in the ratio 2:1 and verify that Q is the mid point of PR .
02:53View SolutionLet P be a point on x2=4y. The segment joining A(0,−1) and P is divided by point Q in the ratio 1:2, then locus of point Q is
02:30View SolutionConsider the points P (3,4,-5) and Q (1,-2,3).Find the co-ordinates of the point which divides the join of P and Q in the ratio a)1:2 internally b)3:2 externally
03:40View SolutionFind the co-ordinates of the point which divides the join of the points (-1,2,3) and (4,-2,5) in the ratio 1 : 2 externally.
03:00View SolutionFind the co-ordinates of the point which divided the join of P(5,-2) and Q(9,6).
internally in ratio 3:105:06View SolutionFind the co-ordinates of the point which divided the join of P(5,-2) and Q(9,6).
externally in ratio 3:103:39View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
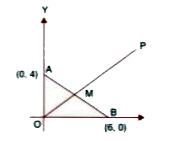
co-ordinates of P01:42View Solution

