Bosco wishes to start a 200m2 rectangular vegetable garden. Since he has only 50 m barbed wire, he fences three sides of the rectangular garden letting his house compound wall act as the fourth side of the fence. Find the dimensions of the garden.
To find the dimensions of Bosco's rectangular vegetable garden, we will follow these steps:
Step 1: Define Variables
Let:
- L = length of the garden (in meters)
- B = breadth of the garden (in meters)
Step 2: Set Up the Equations
Since the area of the garden is given as 200m2, we can write the equation:
L×B=200(1)
Bosco has 50 meters of barbed wire to fence three sides of the garden. The fencing will cover the length and two breadths, so we can write:
L+2B=50(2)
Step 3: Solve for One Variable
From equation (2), we can express L in terms of B:
L=50−2B(3)
Step 4: Substitute in the Area Equation
Now, substitute equation (3) into equation (1):
(50−2B)×B=200
Step 5: Expand and Rearrange
Expanding the equation gives:
50B−2B2=200
Rearranging this, we get:
2B2−50B+200=0
Step 6: Simplify the Quadratic Equation
Dividing the entire equation by 2 simplifies it:
B2−25B+100=0(4)
Step 7: Factor the Quadratic Equation
Now we will factor equation (4). We need two numbers that multiply to 100 and add up to −25. The factors are:
(B−20)(B−5)=0
Step 8: Solve for B
Setting each factor to zero gives us:
B−20=0⇒B=20
B−5=0⇒B=5
Step 9: Find Corresponding Lengths
Now we can find the corresponding lengths using equation (3):
1. If B=20:
L=50−2(20)=10
So one set of dimensions is L=10m and B=20m.
2. If B=5:
L=50−2(5)=40
So another set of dimensions is L=40m and B=5m.
Final Dimensions
Thus, the dimensions of the garden can be:
1. 10m by 20m
2. 40m by 5m
Let:
- L = length of the garden (in meters)
- B = breadth of the garden (in meters)
Since the area of the garden is given as 200m2, we can write the equation:
L×B=200(1)
L+2B=50(2)
From equation (2), we can express L in terms of B:
L=50−2B(3)
Now, substitute equation (3) into equation (1):
(50−2B)×B=200
Expanding the equation gives:
50B−2B2=200
Rearranging this, we get:
2B2−50B+200=0
Dividing the entire equation by 2 simplifies it:
B2−25B+100=0(4)
Now we will factor equation (4). We need two numbers that multiply to 100 and add up to −25. The factors are:
(B−20)(B−5)=0
Setting each factor to zero gives us:
B−20=0⇒B=20
B−5=0⇒B=5
Now we can find the corresponding lengths using equation (3):
1. If B=20:
L=50−2(20)=10
So one set of dimensions is L=10m and B=20m.
L=50−2(5)=40
So another set of dimensions is L=40m and B=5m.
Thus, the dimensions of the garden can be:
1. 10m by 20m
2. 40m by 5m
Topper's Solved these Questions
Similar Questions
A farmer wishes to grow a 100m2 rectangular vegetable garden. Since he has with the only 30 m barbed wire, the fences three sides of the rectangular garden letting compound wall of his house act as the fourth side-fence. Find the dimensions of his garden.
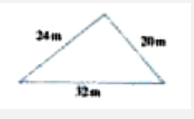
View SolutionFind the cost of fencing a triangular garden with sides 20m,24m and 32m at the rate of 142 per metre.
View SolutionThe length of a rectangular garden is 3 times its width. If the width is 45 m, find the cost of surrounding it with a fence at 18 per metre.
View SolutionFrank the Fencemaker needs to fence in a rectangular yard. He fence in three of four sides of the yard. The unfenced side of the yard is 40 feet long. The yard has an area of 280 square feet. What is the length , in feet, of the fence that Frank installs?
View SolutionReeta wants to fence the graden in front of her house on three sies. The dimensions of the three sides are 14 m, 12 m, and 19m. Find the cost of fencing the garden at the rate of Rs 110 per meter.
View SolutionA rectangular garden is 175 m long and 96 m broad . Find the cost of fencing it at Rs.17.50 per metre .Also ,find the cost of ploughing it at Rs. 4.50 paise per square metre.
View SolutionA rectangular plot of land measures 150m by 250m. How much wire is needed in all if each side is to be fenced with three rows of wire?
View SolutionPriti takes seven rounds of a triangular garden with sides 150m, 120 m, and 100 m. Nisha takes 4 rounds of a rectangular garden with length 500 m and breadth 200 m. Who walks more and by how much?
View SolutionRavish owns a plot of rectangular shape. He has fenced it with a wire of length 750m. The length of the plot exceeds the breadth by 5m. Find the length and breadth of the plot.
View SolutionA rectangular garden is 120 m long and 65 m broad .A path of uniform width of 5 m has to be constructed around it on its outside .Find the cost of gravelling the path at Rs. 11.40 per m2.
View Solution
