Question

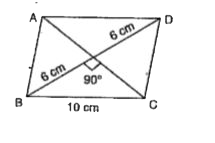
The perimeter of a rhombus is 20 cm. The length of one of its diagonal is 6 cm. What is the length of the other diagonal ?

Options

A. 6 cm
B. 9 cm
C. 8 cm
D. 10 cm

Answer

C

Explanation

To solve the problem step-by-step, we need to find the length of the other diagonal of the rhombus given its perimeter and one diagonal.

Step 1: Understand the properties of a rhombus
A rhombus has four equal sides and its diagonals bisect each other at right angles (90 degrees).

Step 2: Calculate the length of one side of the rhombus
The perimeter of the rhombus is given as 20 cm. Since all sides are equal, we can find the length of one side (s) using the formula for the perimeter of a rhombus:
\( \text{Perimeter} = 4s \)
So,
\( 4s = 20 \implies s = \frac{20}{4} = 5 \text{ cm} \)

Step 3: Set up the relationship between the diagonals
Let the length of the diagonals be \(d_1\) and \(d_2\). We know that one diagonal \(d_1 = 6\) cm. The diagonals bisect each other, so each half of the diagonals will be:
\( AO = \frac{d_1}{2} = \frac{6}{2} = 3 \text{ cm} \)
Let \(d_2\) be the other diagonal, then:
\( BO = \frac{d_2}{2} \)

Step 4: Use the Pythagorean theorem
In triangle AOB, we can apply the Pythagorean theorem since the diagonals intersect at right angles:
\( AB^2 = AO^2 + BO^2 \)
Substituting the known values:
\( 5^2 = 3^2 + \left(\frac{d_2}{2}\right)^2 \)
This simplifies to:
\( 25 = 9 + \left(\frac{d_2}{2}\right)^2 \)
\( 25 - 9 = \left(\frac{d_2}{2}\right)^2 \)
\( 16 = \left(\frac{d_2}{2}\right)^2 \)

Step 5: Solve for \(d_2\)
Taking the square root of both sides:
\( \frac{d_2}{2} = 4 \implies d_2 = 8 \text{ cm} \)

Conclusion
The length of the other diagonal \(d_2\) is 8 cm.