The function for exchanging Americal dollars for Singapore Dollar on a given day isd f(x)=1.23x, where x represents the number of Americal dollars. On the same day the function for exchanging Singapore Dollar to Indian Rupee is g(y)=50.50y, where y represents the number of Singapore dollars. Write a function which will give exchange rate of Americal dollars in terms of Indian rupee.
The correct Answer is:(gof)(x)=62.115x
Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONSBOOK - NCERT TAMILCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 1.5
25 Videos
- SETS, RELATIONS AND FUNCTIONSBOOK - NCERT TAMILCHAPTER - SETS, RELATIONS AND FUNCTIONSEXERCISE - EXERCISE -1.2
10 Videos
- SETSBOOK - NCERT TAMILCHAPTER - SETSEXERCISE - MISCELLANEOUS EXERCISE ON CHAPTER 1
26 Videos
- STATISTICSBOOK - NCERT TAMILCHAPTER - STATISTICSEXERCISE - Miscellaneous Exercise On Chapter 15
7 Videos
Similar Questions
Number of points of discountinuity of y=[sinx]x∈[0,2π) where [.] represents greatest integer function
View Solutiony=−x2+120x−2,000
the equation above gives the profit in dollars, y, a coat manufacturer earns day where x is the number of coats sold. What is the maximum profit he earns in dollars?
View Solution
Knowledge Check
The graph below shows historical exchange rates between the Indian Rupee ( INR) and the US Dollar ( USD) between January 9 and February 8 of a parrticular year .
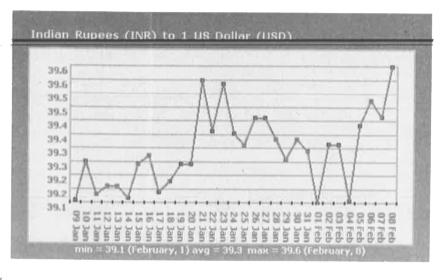
John had 100 dollars. The exchange rate converts the amount in US dollars to a number in Indian Rupees by directly multiplying by the value of the exchange rate. By what amount did John's $100 increase in terms of Indian Rupees from Jan.9 to Fed. 8?A5B10C15D50The original price of a shirt is x dollars. During a sale , the original price is marked down y percent. On the last day of the sale , an additional discount of z percent off the sale price is offered. Which of the following represents the price of the shirt , in dollars , after the additional discount ?
Axyz(100)(100)Bx(1−y)(1−z)100Cx(1−y100)(1−z100)Dx(1−y+z100)A poor , frustrated artist named Fresco created a plan to make money. He collected trash, repurposed it into sculptures, then asked various celebrities to write and paint on these trash objects, which he then sold on his own as modern high art. The chart below separately shows the cost and revenue of his plan. The linear cost function, C(x) , represents the total money spent to make and market the art , while the linear revenue function, R(x) , shows the amount of money he has made in sculpture sales.
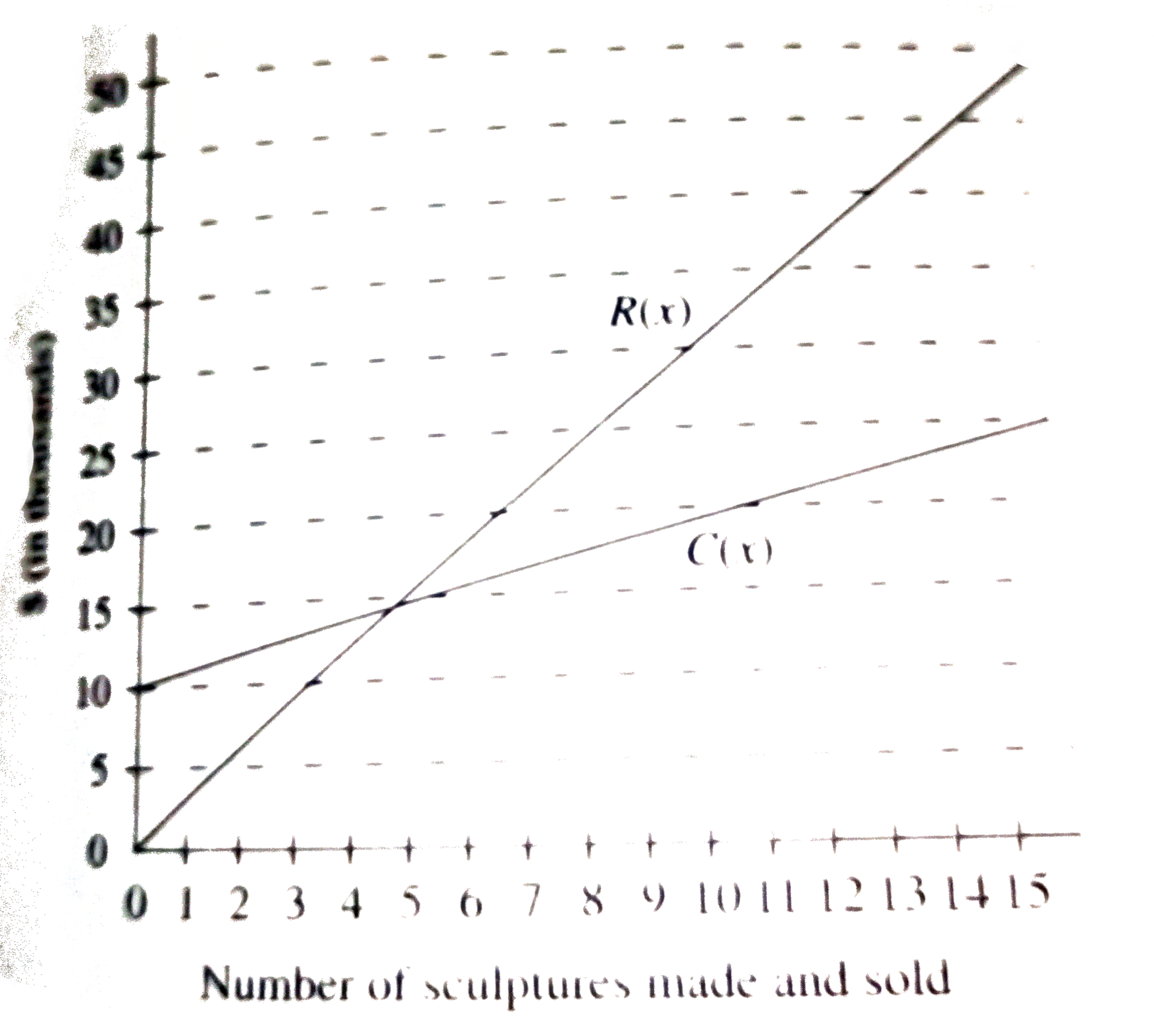
The selling price of each trash sculpture is an integer number of dollars . According to the revenue function , what is the selling price of one trash sculpture ?A$1,000B$1,667C$2,000D$3,000
Exchange rate of U.S. dollar vis-a -vis Indian rupee (i.e. 1 U.S. dollar = so many Rs) from April to Dec . 2002 is given below . Find the range and the coefficient of range.

View SolutionQuestion 1 and 2 refer to the information and graph below.
Let function f be defined by the graph in the accompanying figure.

Q. Let m represents the number of points at which the graphs of y=f(x)andg(x)=3 intersect. Let n represents the number of points at which the graphs of y=f(x)−1andg(x)=3 intersect. What is the value of m+n?
View SolutionSuppose that f is a differentiable function with the property that f(x+y)=f(x)+f(y)+xyandlimh→01hf(h)=3, where [.] represents greatest integer function, then
View SolutionOn January 1, a share of a certain stock costs of $180. Each month decreased by one-third. If x represents the time, in months, and y represents the cost of the stock, in dollars, which graph best represents the cost of a share over the following 5 months?
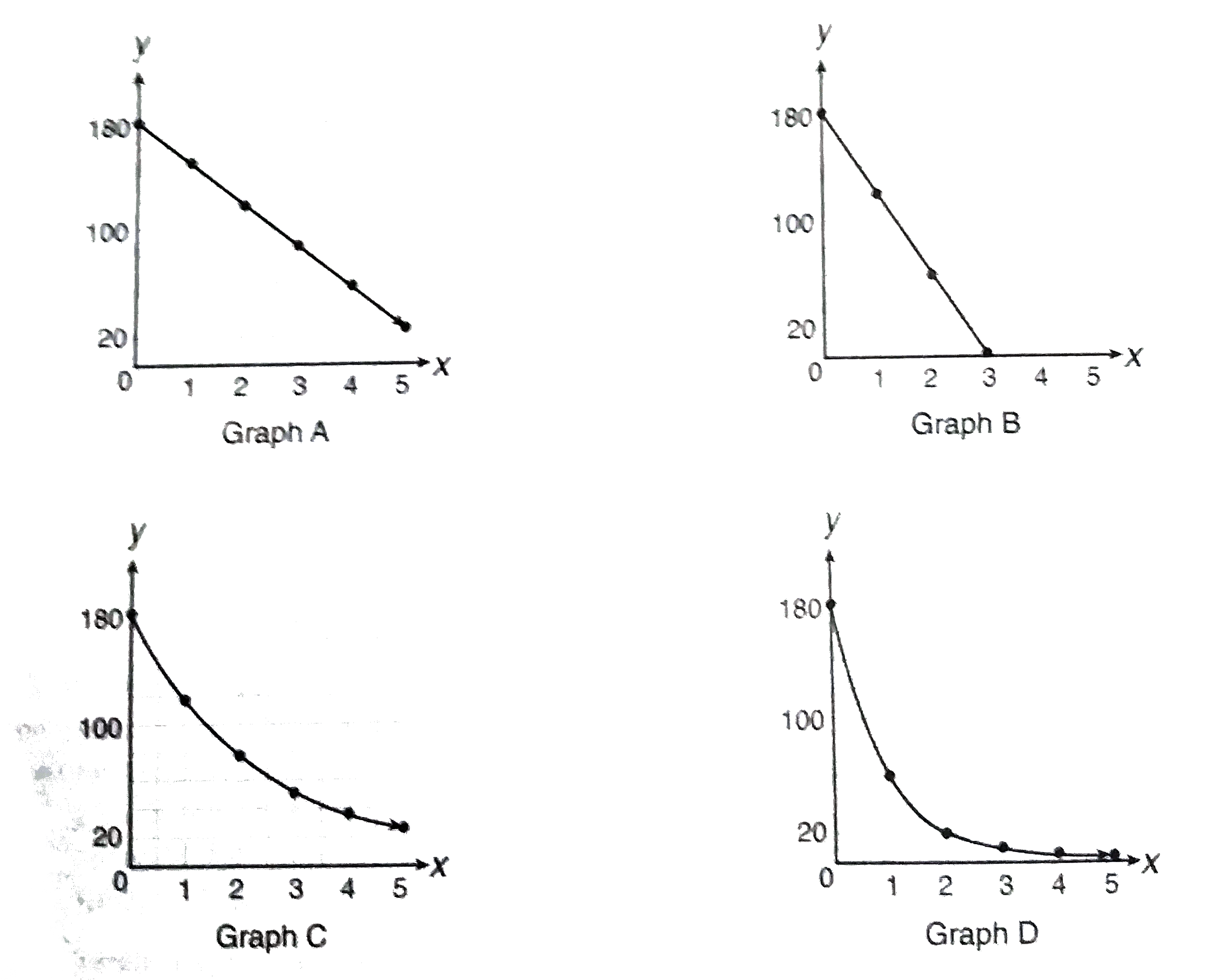
View Solutiony=−75x+5,000
the equation above models the amount of money y, in dollars, remaining in Bo's bank account x days after the start of the fall semester. The amount of money in Bo's bank account is based on the money he earned over the summer and how much he spends per day during the fall semester. When the equation is graphed in the xy-plane , what does the slope of the graph represent in terms of the model?
View Solution
