If a particle moves in a potential energy field U=U0−ax+bx2, where a and bare positive constants, obtain an expression for the force acting on it as a function of position. At what point does the force vanish? Is this a point of stable equilibrium? Calculate the force constant, time-period and frequency of the particle.
As we know, force acting on the particle is given by
F=−dUdx=−ddx(U0−ax+bx2), where, F=a−2bx
(ii) The force vanishes at the point where dUdx=0, i.e., where a−2bx=0. So that, 2bx=a
Or, x=a2b
which gives the position of the point where the force vanishes.
(iii) We have d2Udx2=2b So that, b being positive, the point x=a2b represents the points of minimum potential energy on the energy curve of the particle. It is, therefore, a point of stable equilibrium.
(iv) From the expression for force F in (i) above, it is clear that it is a linear restoring force and the force constant C is therefore equal to 2b.
(v) The time-period of the particle, T=2π√1/μ
where, as we know, μ=Cm=2bm.
So that, T=2π√12bm=2π√m2b
And, therefore, frequency of the particle, n=1T=12π√2bm
Similar Questions
If a particle moves in a potential energy held U=U0−ax+bx2, where are a and b particle constants obtain an expression for the force acting on if as a function of position. At what point does the force vanish? Is this a point of stable equilibrium ?
Calculate the force constant and frequency of the particle.
View SolutionIf a partical moves in a potential energy held U=U0−ax+bx2, where are a and b partical constents obtian an expression for the force acting on if as a function of position. At what point does the force vanish? Is this a point of stable equilibriun ?
Calculate the force constant and friquency of the partical.
View Solution
Knowledge Check
A particle of mass m moves in a one dimensional potential energy U(x)=−ax2+bx4, where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
Aπ√a2bB2√amC√2amD√a2mA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants.For ximplies0, the correct variation of potential energy function U(x) is best represented by.
A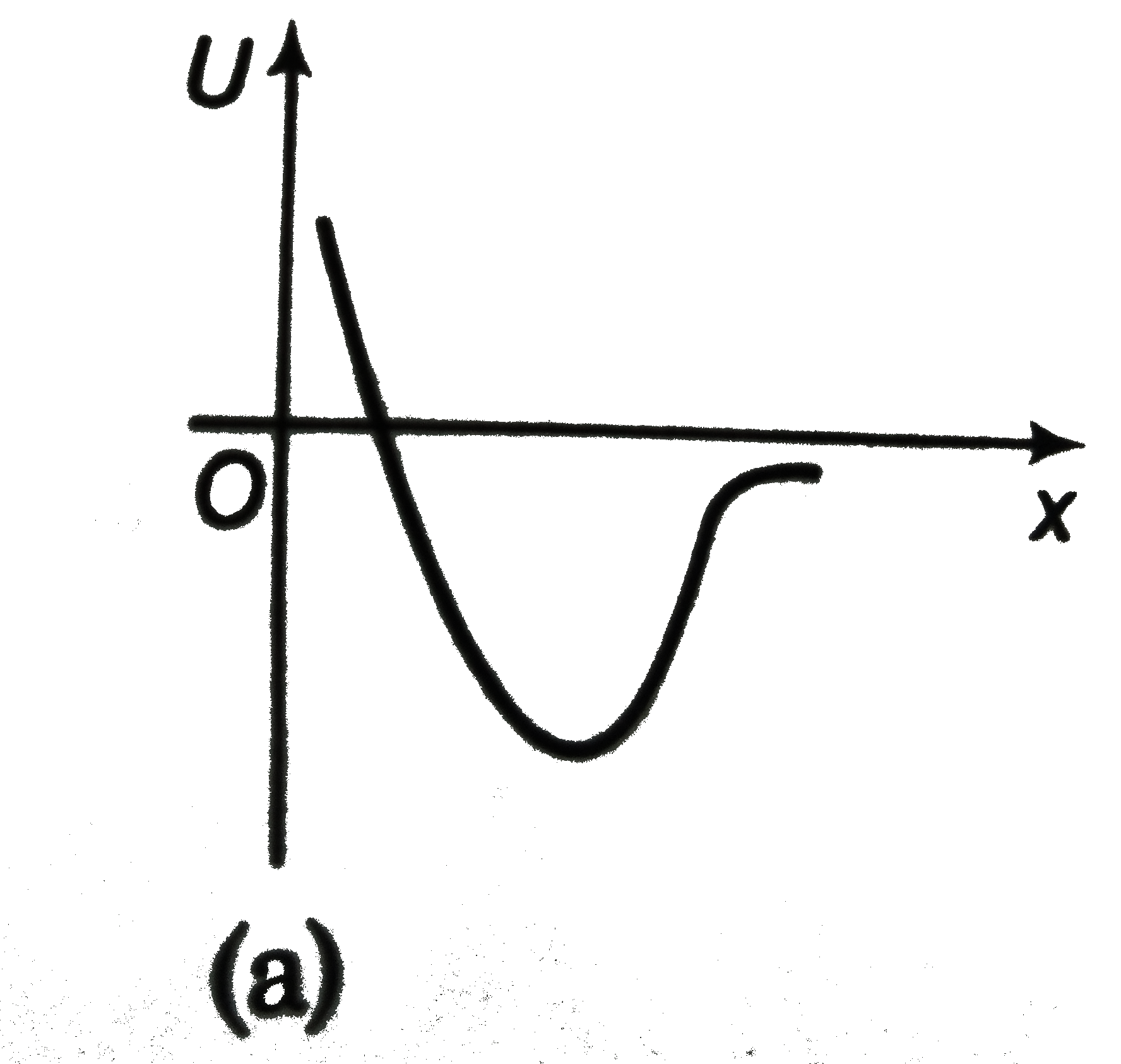 B
B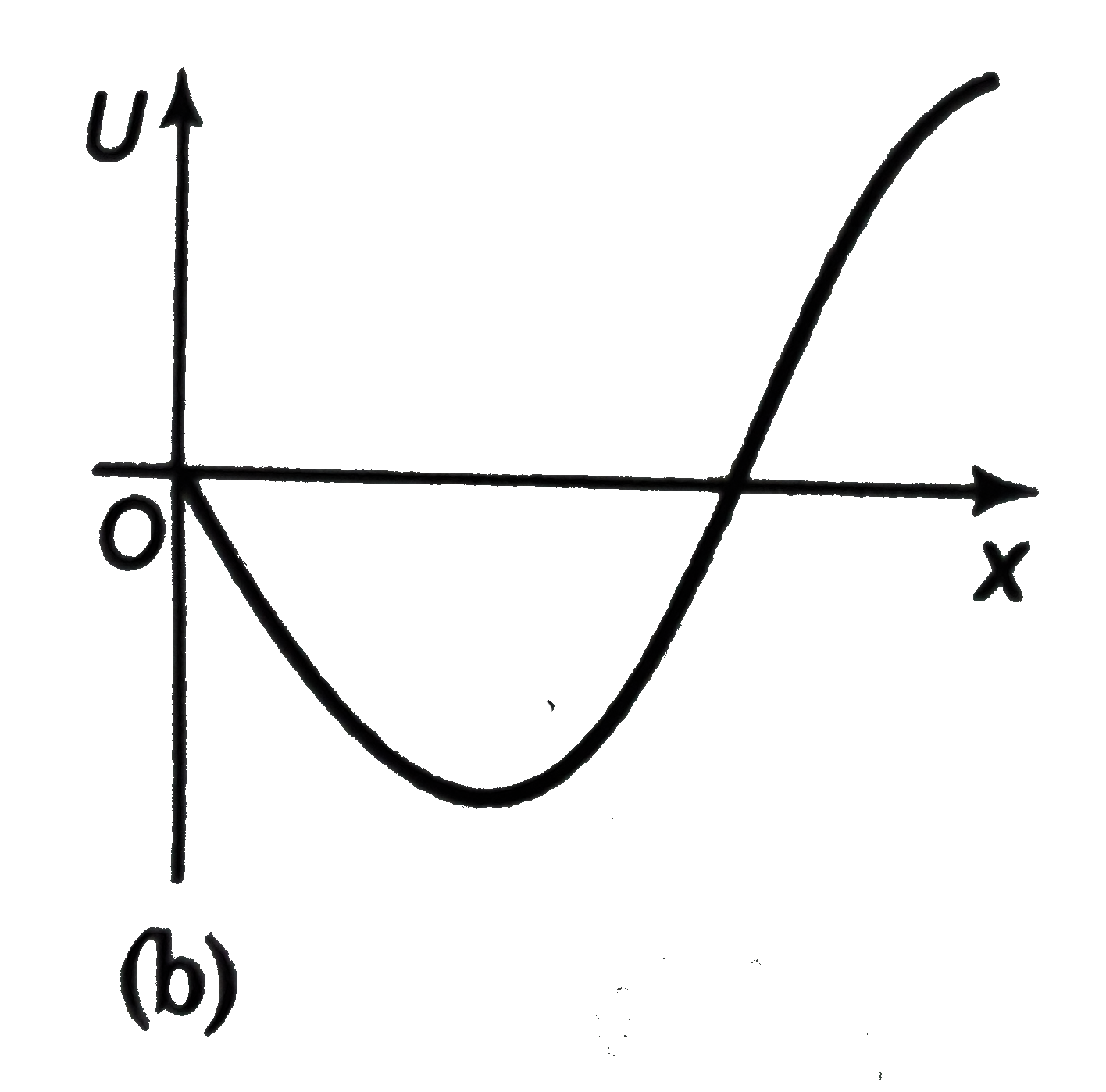 C
C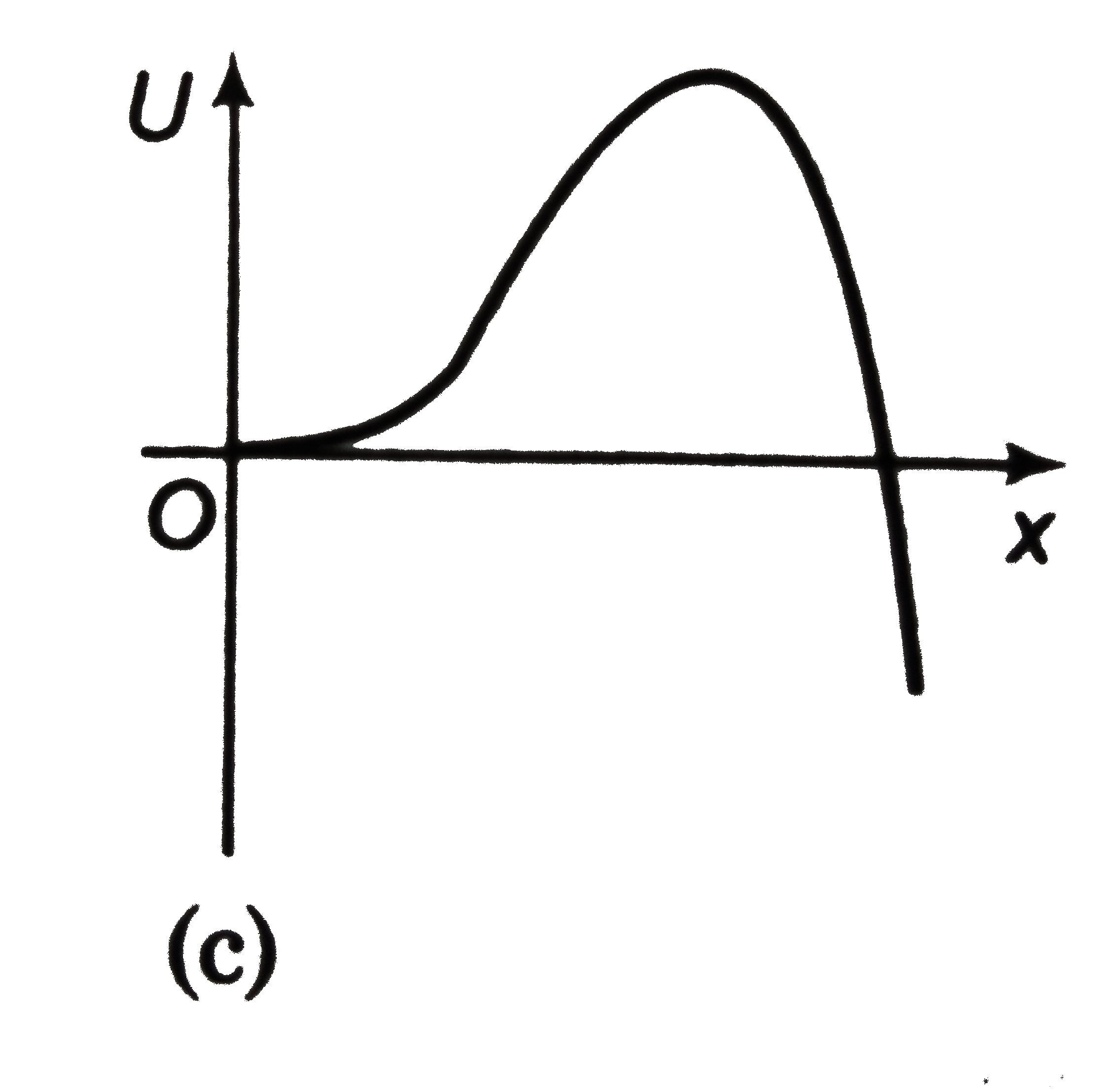 D
D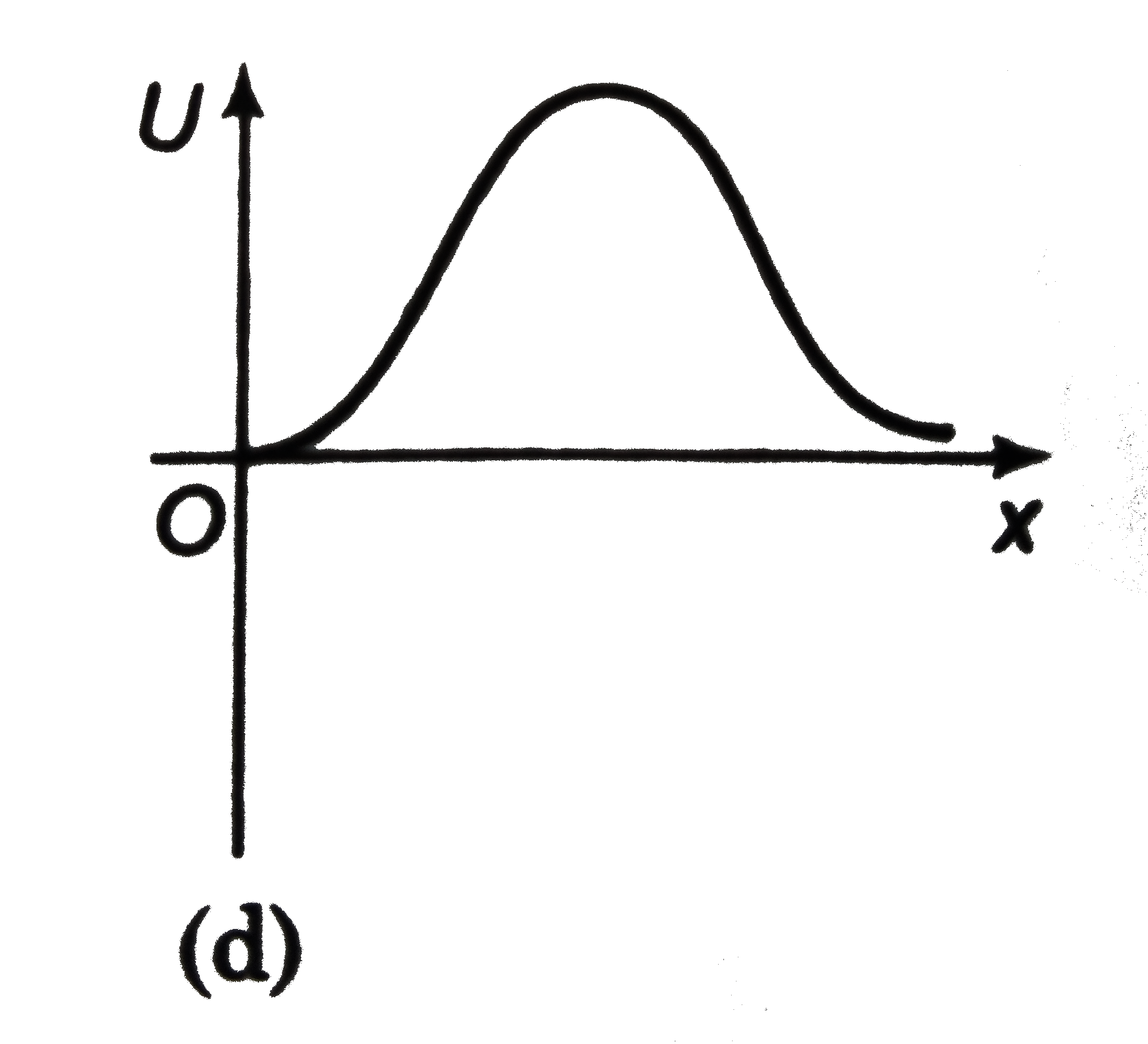
The potential energy for a conservative system is given by
U=ax2−bx
where a and b are positive constants. The law of the force governing the system isAF = constantBF=bx–2aCF=b−2axDF=2ax
If a particle of mass m moves in a potential energy field U=U0−ax+bx2 where U0, a and b are positive constants.Then natural frequency of small oscillations of this particle about stable equilibrium point is 1xπ√bm. The value of x is?
View SolutionA particle of mass m moves in a one dimensional potential energy U(x)=−ax2+bx4, where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants., the correct variation of potential energy function U(x) is best represented by.
View SolutionA particle of mass m oscillates with a potential energy U=U0+αx2, where U0 and α are constants and x is the displacement of particle from equilibrium position. The time period of oscillation is
View SolutionA particle is acted upon by a force given by F=−αx3−βx4 where α and β are positive constants. At the point x = 0, the particle is –
View Solution
