A charge (Q) is kept inside an open cylinder at the centre. The cylinder has a diameter of L and height of 2L. What is the toal flux going through the surface of the cylinder?
Concept: Flux is a scalar quantity. The total flux through the closed cylindrical Gaussian surface (open cylinder + two circular areas) can be found using Gauss.s law. From this, if we subtract the flux through the two closing circular areas, the total flux through the open cylinder can be obtained. A cylinderical Gaussian surface is chosen as shown below.
Let ϕnet be the flux through the Gaussian surface considered. Let total charge enclosed be Q. From Gauss.s law, Qnet=Qε0
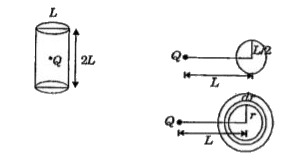
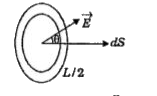
Calculation of flux of the electric field due to Q, through the circular areas: The surface through which electric flux is required is open. Consider a small ring of radius r and thickness dr as shown. The plane can be considered to be made of a collection of such rings.
Now, let us calculate the flux through the ring of radius r.
∫dϕ=∫→E.d→S
dS=2πrdr
E=14πε0Q(L2+r2)

∫dϕ=L/2∫0EdS.cosθ,∫dϕ=L/2∫0Q(2πrdr)cosθ4πε0(L2+r2)
∫dϕ=Q2ε0L/2∫0rdr(L2+r2)L√L2+r2⇒ϕ=QL2ε0L/2∫0rdr(L2+r2)3/2=QL2ε0[−1√L2+r2]L/20
⇒ϕ=QL2ε0[1L−1√L2+L2/4]=Q2ε0[1−2√5]
Flux through the open cylinder is, ϕ1=ϕnet−2ϕ=Qε0−Qε0[1−2√5]
ϕ1=2Q√5ε0
Similar Questions
Knowledge Check
- Question 1 - Select One
a point charge q is placed at the centre of a cylinder of length L and radius R the electric flux through the curved surface of the cylinder is
Aqε0L√L2+R2Bqε0L√L2+2R2Cqε0L√L2+4R2Dq2ε0 - Question 2 - Select One
The diameter of a cylinder is 28 cm and its height is 20 cm . The total surface area of the cylinder is
A2993cm2B2992cm2C2292 cm2D2229 cm2 - Question 3 - Select One
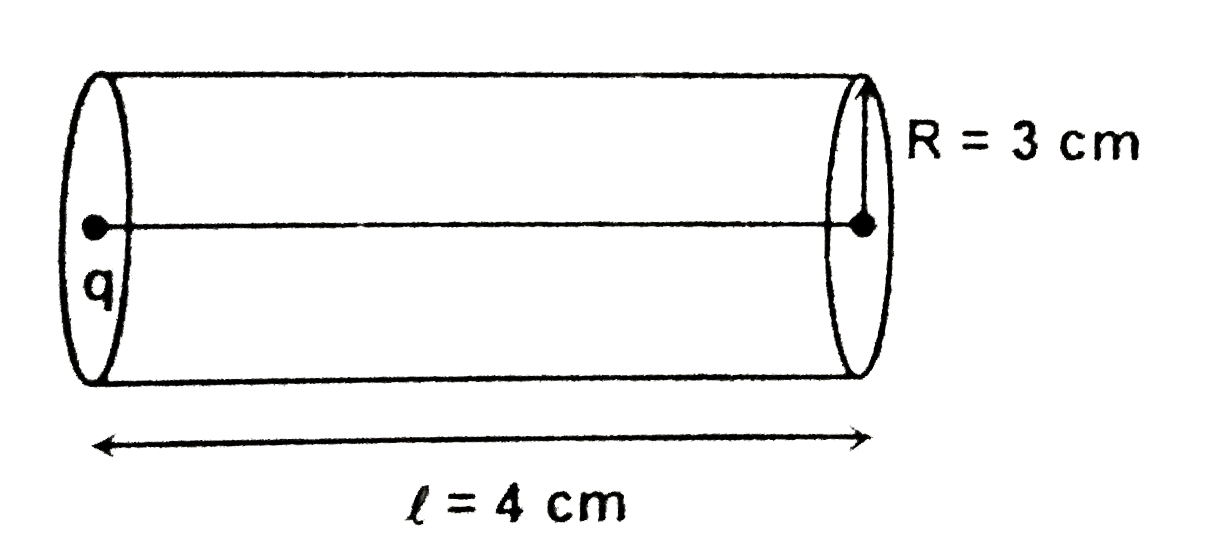
A point charge 'q' is placed at the centre of left circular end of a cylinder of length l=4cm and radius R=3 cm shown. Then the electric flux through the curved surface of the cylinder isAq5ε0B2q5ε0C3q5ε0D4q5ε0
A closed circular cylinder has diameter 20cm and height 30cm. Find the total surface area of the cylinder is
View Solution
A point charge 'q' is placed at the centre of left circular end of a cylinder of length l=4cm and radius R=3 cm shown. Then the electric flux through the curved surface of the cylinder isView SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View Solution

