An electric dipole coincides on z axis and its mid point is at the origin on the cartesian co-ordinate system. The electric field at an axial point at a distance z from origin is →E(z) and electric field at an equatorial point at a distance y from origin is →E(y). Then
∣∣
∣∣→E(z)→E(y)∣∣
∣∣(y=z>>a) = ......................
1
2
4
3
The correct Answer is:B
Theory related question
Similar Questions
An electric dipole coincides on Z-axis and its mid-point is on origin of the coordinates system. The electric field at an axial point at a distance z from origin is E(z) and electric field at an equatorial point at a distance y from origin is E(y). Here, z=y>>a, so ∣∣∣E(z)E(y)∣∣∣=... 1 4 3 2
View SolutionA disc is kept on xy plane with centre at origin. Find electric field at a point with distance Z from origin on z-axis.
View Solution
Knowledge Check
An electric dipole coincides on Z-axis and its mid-point is on origin of the coordinates system. The electric field at an axial point at a distance z from origin is E(z) and electric field at an equatorial point at a distance y from origin is E(y). Here, z=y>>a, so ∣∣∣E(z)E(y)∣∣∣=...
A1B4C3D2Electric field at a far away distance r on the axis of dipole is →E0. What is the electic field at a distance 24 on perpendicular bisector?
A→E016B−→E016C→E08D−→E08If the intensity of electric field at a distance x from the centre in axial position of small electric dipole is equal to the intensity at a distance y in equatorial position, then
Ax=yBx=y/2Cy=x/22/3Dy=x/21/3
A dipole is placed at origin of coordinate system as shown in figure, find the electric field at point P(0,y)
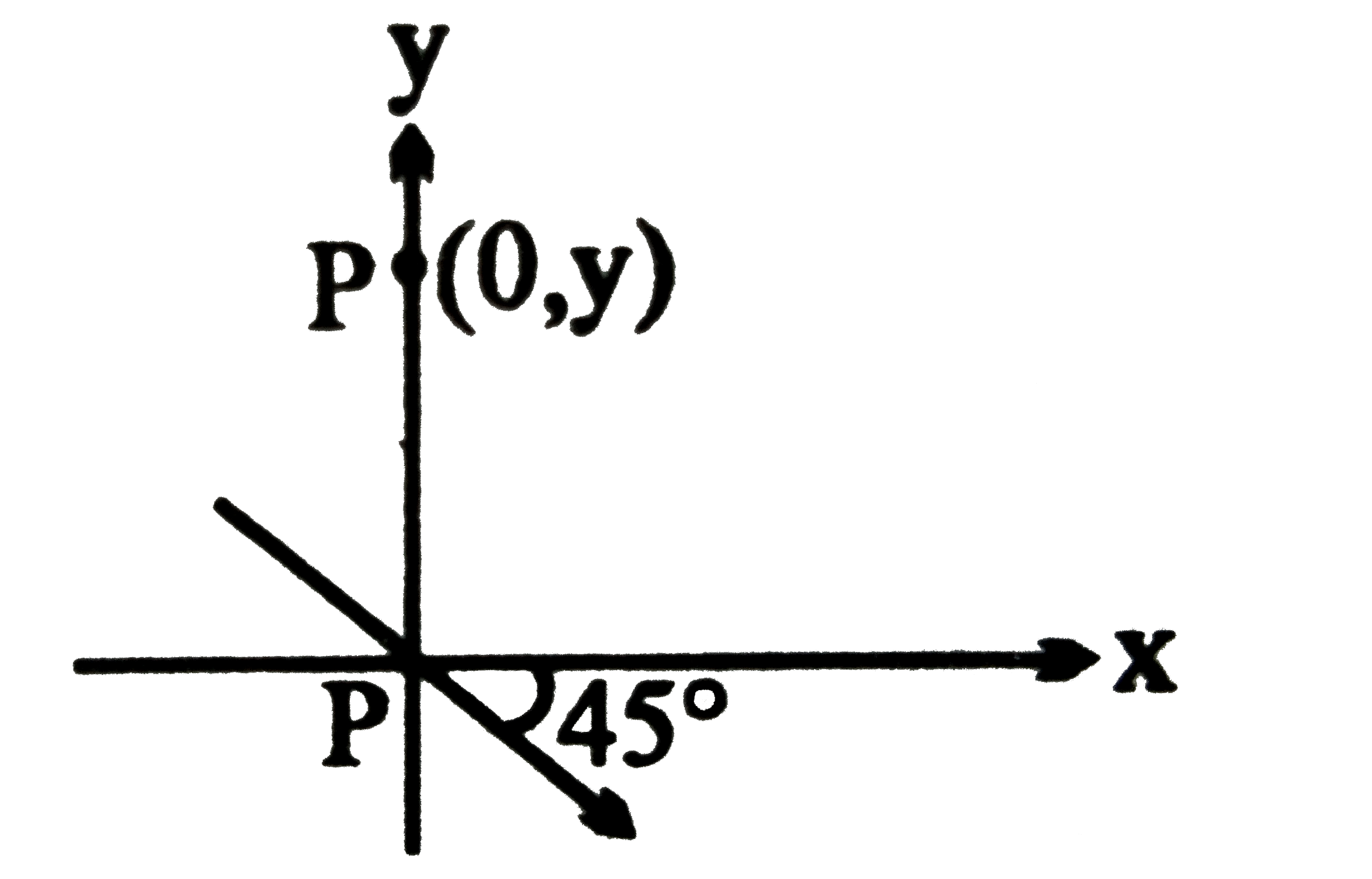 .
.
View SolutionA dipole is placed at origin of corrdinate system as shown in figure, find the electric field at point P(0,y)
 .
.
View SolutionIf the intensity of electric field at a distance x from the centre in axial position of small electric dipole is equal to the intensity at a distance y in equatorial position, then
View SolutionThe electirc potential at a point (x,y,z) is given by
V=−x2y−xz3+4
The electric field →E at that point is
View SolutionThe electirc potential at a point (x,y,z) is given by
V=−x2y−xz3+4
The electric field →E at that point is
View Solution
