If A=[12−13−25] , apply R1↔R2 and then C1→C1+2C3 on A.
The correct Answer is:A~[3+2(5)−251+2(−1)2−1]∴A~[13−25−12−1]
Similar Questions
If A=⎡⎢⎣1−13210331⎤⎥⎦ then apply R1→R2 and then C1→C1+2C3 on A
View SolutionThere circle C1,C2 and C3 with radii r1,r2 and r3 (where r1<r2<r3) are placed as shown in the given figure. What is the value of r2?
तीन वृत्तC1,C2 तथा C3 जिनको त्रिज्याएँ r1,r2 तथा r3 है, (जहाँ r1<r2<r3 ) को दी हुई आकृति में दर्शाया गया है। r2, का मान क्या है?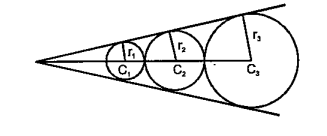
View Solution
Knowledge Check
- Question 1 - Select One
If A=[12−13−25], then first R1↔R2 and then C1→C1+2C3 on A gives
A[−12−113−25]B[3−2512−1]C[−12−113−25]D[13−25−12−1] - Question 2 - Select One
If A=[1 2−13−2 5] , then R1↔R2 and C1→C1+2C3 given
A[−132−5−12−1]B[−1−2−1 13−2 5]C[ 13−2 5−1 2−1]D[2−13−52−1−1] - Question 3 - Select One
If A=[10−13], then R1↔R2 on A gives
A[−1310]B[1−103]C[013−1]D[3011]
A 3×3 matrix A, with 1st row elements as 2,-1,-1 respectively, is modified as below to get another matrix B.
R1 elements of A go to R3 of matrix C
R2 elements of A go to R1 of matrix C
R2 elements of A to R1 of matrix C
R3 elements of A go to R2 fo matrix C
Now, below operations are done on C as follow,
C1 elements of C go to C3 of B
C2 elements of C go to C1 of B
C3 elements of C go to C2 of B
It is found that A = B, thenView SolutionIf A=[5413], then C1↔C2 on A gives
View Solution⎡⎢⎣13−2−30−5250⎤⎥⎦=A⎡⎢⎣100010001⎤⎥⎦ then, C2→C2−3C1andC3→C3+2C1 gives
View SolutionIf A=⎡⎢⎣2−332233−22⎤⎥⎦ then
C2→C2+2C1 and then R1→R1+R3 givesView SolutionA 3×3 matrix A, with 1st row elements as 2,-1,-1 respectively, is modified as below to get another matrix B.
R1 elements of A go to R3 of matrix C
R2 elements of A go to R1 of matrix C
R2 elements of A to R1 of matrix C
R3 elements of A go to R2 fo matrix C
Now, below operations are done on C as follow,
C1 elements of C go to C3 of B
C2 elements of C go to C1 of B
C3 elements of C go to C2 of B
It is found that A = B, thenView Solution