Apply the given elementary transformation on each of the following matrices.
A=[5413],C1↔C2, B=[3145]R1↔R2. What do you observe ?
Text Solution
The correct Answer is:A~[4531]B~[4531] The new matrices are equal .
|
Similar Questions
Knowledge Check
If A=[3145], then R1↔R2 on A gives
A[3415]B[4531]C[1354]D[5−1−43]
Using elementary transformations, find the inverse of the matrices A=⎡⎢⎣20−1510013⎤⎥⎦A−1=?
View SolutionUsing elementary transformations (operations), find the inverse of the following matrices, if it exists ⎡⎢⎣2−13−531−323⎤⎥⎦
View SolutionLet A (4,2) , B (6,5) and C (1,4) be the vertices of ΔABC.
What do you observe?
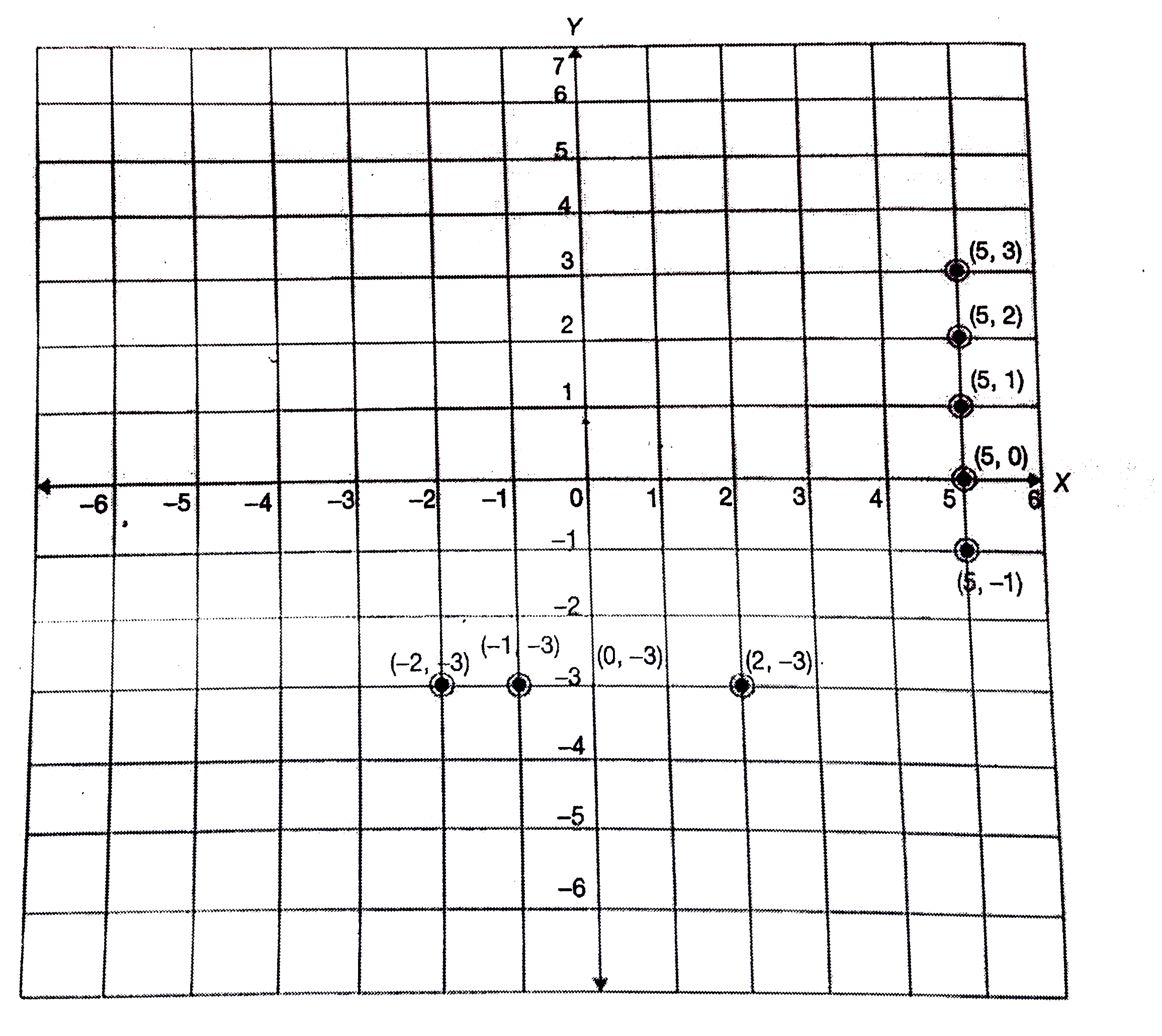
View SolutionPlot the following points on the coordinate plane. What do you observe ?
(a) (−2,−3),(−1,−3),(0,−3),(2,−3)
(b) (5,3),(5,2),(5,1),(5,0),(5,−1)
View SolutionFind the inverse of the matrix A=⎡⎢⎣123245356⎤⎥⎦ by using elementary raw transformations
View SolutionGiven the matrices A=[2113−10024] , B=[97−1354216] and C=[2−431−10945] Verify that (A+B)+C=A+(B+C) .
View SolutionIf [2−365][1023]=[−4−91615]
Write the equation after applying elementary column transformation C2→C2+2C1
View Solution
