Read the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
Identify the correct equation that represents the exponential population growth curve:
dN/dt=IN
dN/dt=rN(K−N/K)
Nt=N0ert
Both (A) are (C )
The correct Answer is:D
To identify the correct equation that represents the exponential population growth curve, we can follow these steps:
1. Understanding Population Growth: Recognize that population growth can occur in two primary patterns: exponential and logistic. Exponential growth happens under conditions of unlimited resources.
2. Defining Exponential Growth: In exponential growth, the rate of change of the population size (dn/dt) is proportional to the current population size (n). This can be expressed mathematically.
3. Mathematical Representation: The equation for exponential growth can be represented as:
dndt=r⋅n
where:
- dndt is the change in population size over time.
- r is the intrinsic rate of natural increase (birth rate minus death rate).
- n is the current population size.
4. Integrating the Equation: To find the population size at any time t, we integrate the equation:
∫1ndn=∫rdt
This leads to:
ln(n)=rt+C
where C is the integration constant.
5. Solving for Population Size: Exponentiating both sides gives:
n=ert+C=eC⋅ert
Letting eC be the initial population size n0, we have:
n=n0ert
6. Final Equation: Therefore, the equation that represents the exponential growth curve is:
n(t)=n0ert
Conclusion:
The correct equation that represents the exponential population growth curve is n(t)=n0ert.
---
dndt=r⋅n
where:
- dndt is the change in population size over time.
- r is the intrinsic rate of natural increase (birth rate minus death rate).
- n is the current population size.
∫1ndn=∫rdt
This leads to:
ln(n)=rt+C
where C is the integration constant.
n=ert+C=eC⋅ert
Letting eC be the initial population size n0, we have:
n=n0ert
n(t)=n0ert
The correct equation that represents the exponential population growth curve is n(t)=n0ert.
Similar Questions
Knowledge Check
Read the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
Identify the incorrect statement :AExponential growth occurs is organism such as lemmings .BLogistic growth is more relistic .CExponential growth has two phases lag and log .DIn logistic growth, population passes well beyond the carrying capacity of ecosystem.Read the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
The equations correctly represents Verhulst-Pearl logistic growth is:AdN/dt=rN(K−N)/KBdN/dt=rN/KCdN/dt=N(K−N)/KDdN/dt=K(K−N)/NRead the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
Study the population growth curves (A and B) in the given graph and select the incorrect statement :
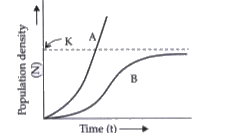 ACurve 'A' shows exponential growth represented by equation dN/dt=rNBCurve 'B' shows logistic growth , represented by equation dN/dt=r(K−N)/KCExponential growth curved is considered as more realistic than the logistic growth curveDCurve 'A' can also be represented by equation Nt=N0en
ACurve 'A' shows exponential growth represented by equation dN/dt=rNBCurve 'B' shows logistic growth , represented by equation dN/dt=r(K−N)/KCExponential growth curved is considered as more realistic than the logistic growth curveDCurve 'A' can also be represented by equation Nt=N0en
Read of the following text and answer the following questions on the basis of the same:
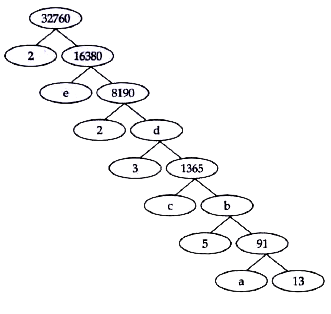
Find the value of c
View SolutionRead of the following text and answer the following questions on the basis of the same:
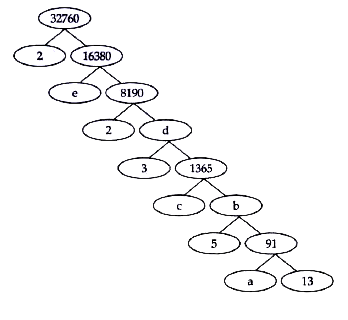
Find the value of d
View SolutionRead of the following text and answer the following questions on the basis of the same:

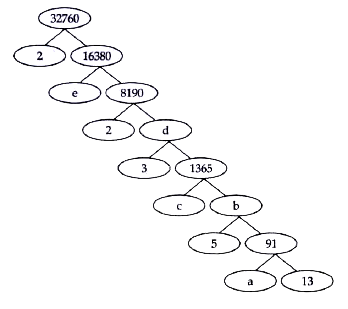
Find the value of e
View SolutionRead the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
The population growth is generally descibed by the following equations :
dN/dt=rN(K−N)/K
What does 'r' represent in the given equation ?
View SolutionWhen resources are unlimited each species has the ability to realise fully its innate potential to grow in number as observed by
View Solution