Two dice are thrown at the same time. Find the probability of getting :
different numbers on both dice.
The correct Answer is:56
To solve the problem of finding the probability of getting different numbers on both dice when two dice are thrown, we can follow these steps:
Step 1: Determine the total number of outcomes
When two dice are thrown, each die has 6 faces. Therefore, the total number of outcomes when throwing two dice is:
Total outcomes=6×6=36
Step 2: Determine the number of favorable outcomes for different numbers
Next, we need to find the number of outcomes where the two dice show different numbers. To do this, we can first calculate the number of outcomes where both dice show the same number.
The pairs where both dice show the same number are:
- (1, 1)
- (2, 2)
- (3, 3)
- (4, 4)
- (5, 5)
- (6, 6)
This gives us a total of 6 outcomes where both dice show the same number.
Step 3: Calculate the number of outcomes with different numbers
To find the number of outcomes where the two dice show different numbers, we subtract the number of same-number outcomes from the total outcomes:
Different outcomes=Total outcomes−Same outcomes=36−6=30
Step 4: Calculate the probability
The probability of getting different numbers on both dice is given by the ratio of the number of favorable outcomes to the total outcomes:
Probability=Favorable outcomesTotal outcomes=3036=56
Final Answer
Thus, the probability of getting different numbers on both dice is:
56
---
When two dice are thrown, each die has 6 faces. Therefore, the total number of outcomes when throwing two dice is:
Total outcomes=6×6=36
Next, we need to find the number of outcomes where the two dice show different numbers. To do this, we can first calculate the number of outcomes where both dice show the same number.
- (1, 1)
- (2, 2)
- (3, 3)
- (4, 4)
- (5, 5)
- (6, 6)
To find the number of outcomes where the two dice show different numbers, we subtract the number of same-number outcomes from the total outcomes:
Different outcomes=Total outcomes−Same outcomes=36−6=30
The probability of getting different numbers on both dice is given by the ratio of the number of favorable outcomes to the total outcomes:
Probability=Favorable outcomesTotal outcomes=3036=56
Thus, the probability of getting different numbers on both dice is:
56
Topper's Solved these Questions
- PROBABILITYBOOK - OSWAL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - BOARD CORNER ( Very Short Answer Type Questions)
2 Videos
- PROBABILITYBOOK - OSWAL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - BOARD CORNER (Short Answer Type Questions)
13 Videos
- PROBABILITYBOOK - OSWAL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - NCERT CORNER ( Exercise-13.2)
10 Videos
- POLYNOMIALS BOOK - OSWAL PUBLICATIONCHAPTER - POLYNOMIALS EXERCISE - SELF -ASSESSMENT
24 Videos
- QUADRATIC EQUATIONSBOOK - OSWAL PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - Passage Based Questions
10 Videos
Similar Questions
Two dice are thrown at the same time. Find the probability of getting :
same number on both dice.
View SolutionTwo dice are thrown at the same time. Find the probability of getting
(i) Same number on both dice.
(ii) different number of both dice.
View SolutionTwo dice are thrown at the same time. Find the probability of getting an even number on the first die
View SolutionTwo dice are thrown at the same time . Find the probability of getting sum dice is 8 .
View SolutionTwo dice are thrown at the same time . Find the probability of getting sum of the dice is 13 .
View SolutionTwo dice are thrown at the same time. Find the probability of getting the sum of the dice is 8.
View Solution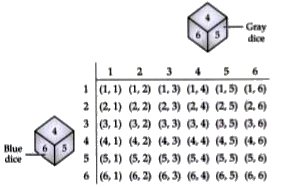
Two dice, one blue and one grey are thrown at the same time.
Find the probability of getting an even number as the sum.
View SolutionTwo dice are thrown at the same time . Find the probability of getting the sum on dice is less than or equal to 12 .
View SolutionTwo dice are thrown at the same time. Determine the probability that the difference of the number on the two dice is 2.
View SolutionTwo dice are thrown at the same time. Determine the probability that the difference of the numbers on the two dice is :
(i) 0. (ii) 2.
View Solution
