A wire of resistance 5Ω is bent in the form of a closed circle. Find the resistance across the diameter of the circle.
To find the resistance across the diameter of a wire bent in the form of a closed circle, we can follow these steps:
1. Understanding the Problem:
- We have a wire with a total resistance of R=5Ω that is bent into a circular shape. We need to find the resistance across the diameter of this circle.
2. Dividing the Wire:
- When the wire is bent into a circle, it can be thought of as being divided into two equal semicircular parts. Each semicircle will have a resistance of R1 and R2.
3. Calculating Resistance of Each Semicircle:
- Since the total resistance of the wire is 5Ω, the resistance of each semicircular part (from point A to B) will be:
R1=R2=R2=5Ω2=2.5Ω
4. Using the Parallel Resistance Formula:
- The two semicircular resistances are in parallel when considering the resistance across the diameter. The formula for equivalent resistance Req for two resistors in parallel is given by:
1Req=1R1+1R2
5. Substituting Values:
- Substitute R1 and R2 into the formula:
1Req=12.5+12.5=22.5=252=45
6. Finding the Equivalent Resistance:
- Now, take the reciprocal to find Req:
Req=54Ω
Final Answer:
The resistance across the diameter of the circle is 54Ω or 1.25Ω.
---
- We have a wire with a total resistance of R=5Ω that is bent into a circular shape. We need to find the resistance across the diameter of this circle.
- When the wire is bent into a circle, it can be thought of as being divided into two equal semicircular parts. Each semicircle will have a resistance of R1 and R2.
- Since the total resistance of the wire is 5Ω, the resistance of each semicircular part (from point A to B) will be:
R1=R2=R2=5Ω2=2.5Ω
- The two semicircular resistances are in parallel when considering the resistance across the diameter. The formula for equivalent resistance Req for two resistors in parallel is given by:
1Req=1R1+1R2
- Substitute R1 and R2 into the formula:
1Req=12.5+12.5=22.5=252=45
- Now, take the reciprocal to find Req:
Req=54Ω
The resistance across the diameter of the circle is 54Ω or 1.25Ω.
Similar Questions
A wire of resistance 5 Ohms is bent in the form of a closed circle. What is the effective resistance between the two points at ends of any diameter of the circle?

View Solution(a) Justify the following statements
(i) Tungsten is used exclusively for filament by electric lamps
(ii) We do not use series arrangement for domestic circuits.
(b) A wire of resistance 8Ω is bent in the form of a closed circle. What is the effective resistance between two points A and B at the ends of any diameter of the circle ?
View Solution
Knowledge Check
A wire has resistance of 12Ω. It is bent in the form of a circle. The effective resistance across any diameter is equal to
A12ΩB6ΩC3ΩD24ΩA uniform wire of resistance 36Ω is bent in the form of a circle. The effective resistance across the points A and B is
 A5ΩB15ΩC7.2ΩD30Ω
A5ΩB15ΩC7.2ΩD30ΩA uniform wire of resistance 18Ω is bent in the form of a circle. The effective resistance across the points a and b is
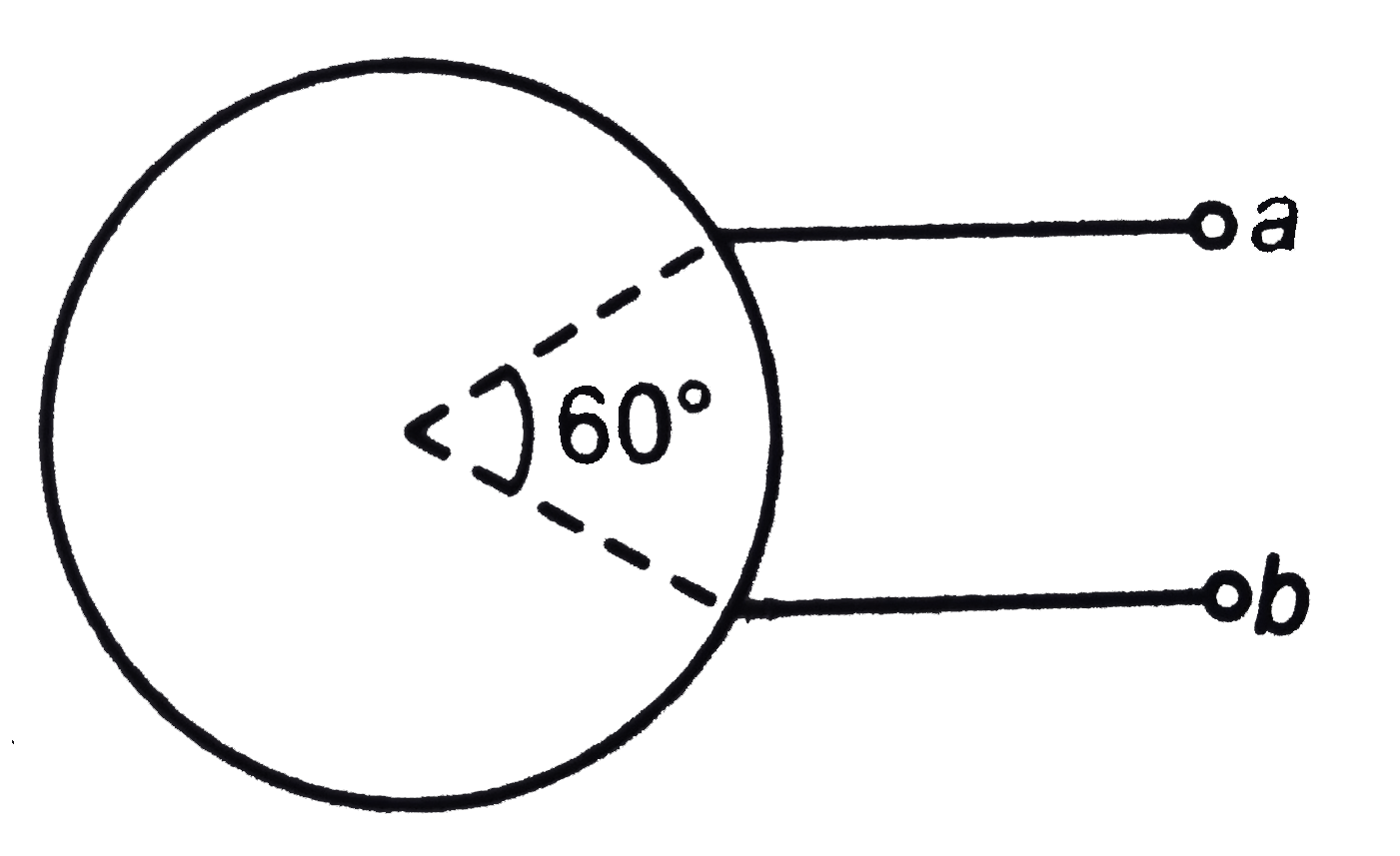 A3ΩB2ΩC2.5ΩD6Ω
A3ΩB2ΩC2.5ΩD6Ω
A wire of resistance 4R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
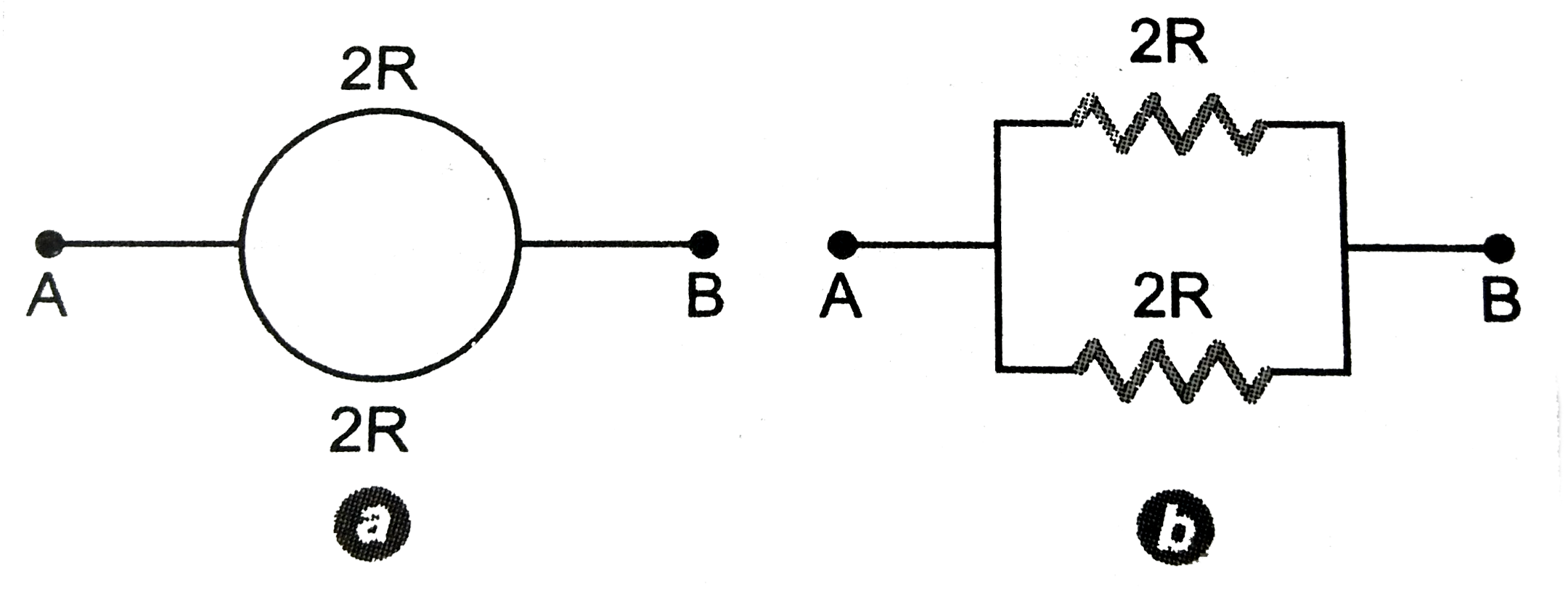
View SolutionA wire of resistance 6R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
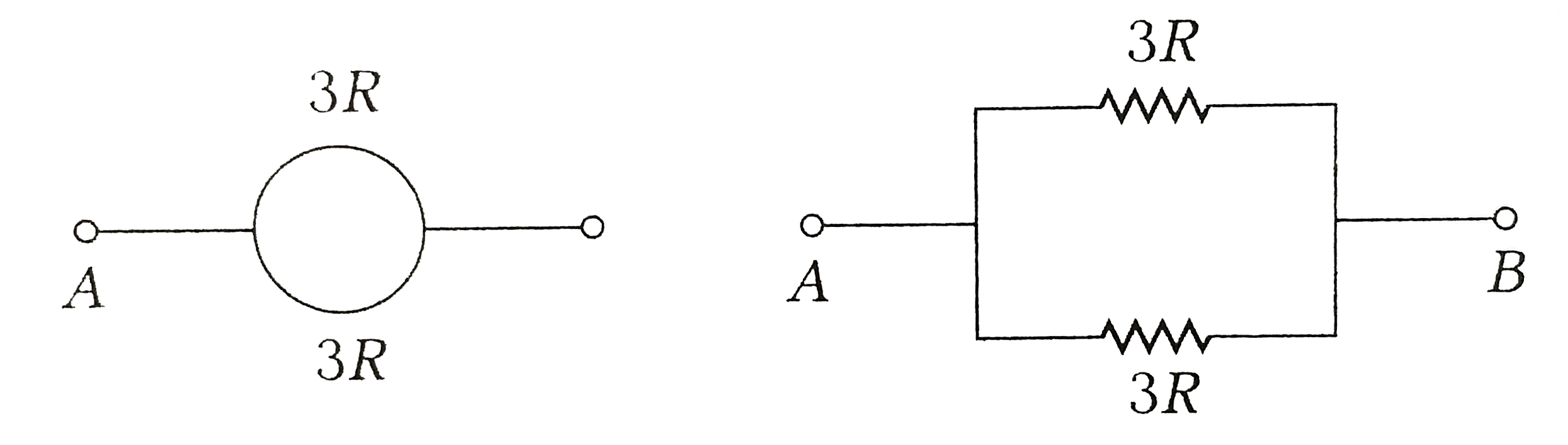
View SolutionA uniform wire of resistance 2R is bent in the form of a circle. The effective resistance between the ends of any diameter of the circle is
View SolutionA wire of resistance 16Ω is bent in the form of a circle. What is the effective resistance between diametrically opposite points?
View SolutionA uniform wire os resistance 12Ω is bent to form a circle. Effective resistance across two diametrically opposite points is
View Solution
