Three planets revolve round the sun once in 200, 250, 300 days respectively in their own orbits. When do they all come relatively to the same position as at a certain point of time in their orbits ?
After 3000 days
After 2000 days
After 1500 days
After 1200 days
To find out when the three planets will come back to the same position in their orbits, we need to calculate the least common multiple (LCM) of their revolution periods. The planets revolve around the sun in 200 days, 250 days, and 300 days respectively.
1. Identify the periods of revolution:
- Planet A: 200 days
- Planet B: 250 days
- Planet C: 300 days
2. Find the prime factorization of each period:
- 200 = 2^3 × 5^2
- 250 = 2^1 × 5^3
- 300 = 2^2 × 3^1 × 5^2
3. Determine the highest power of each prime factor:
- For the prime number 2: The highest power is 2^3 (from 200).
- For the prime number 3: The highest power is 3^1 (from 300).
- For the prime number 5: The highest power is 5^3 (from 250).
4. Calculate the LCM using the highest powers:
LCM=23×31×53
5. Calculate each component:
- 23=8
- 31=3
- 53=125
6. Multiply these together:
LCM=8×3×125
7. Calculate step-by-step:
- First, calculate 8×3=24
- Then, calculate 24×125=3000
8. Conclusion:
The three planets will come back to the same position after 3000 days.
Final Answer:
After 3000 days, all three planets will be at the same position in their orbits.
---
- Planet A: 200 days
- Planet B: 250 days
- Planet C: 300 days
- 200 = 2^3 × 5^2
- 250 = 2^1 × 5^3
- 300 = 2^2 × 3^1 × 5^2
- For the prime number 2: The highest power is 2^3 (from 200).
- For the prime number 3: The highest power is 3^1 (from 300).
- For the prime number 5: The highest power is 5^3 (from 250).
LCM=23×31×53
- 23=8
- 31=3
- 53=125
LCM=8×3×125
- First, calculate 8×3=24
- Then, calculate 24×125=3000
The three planets will come back to the same position after 3000 days.
After 3000 days, all three planets will be at the same position in their orbits.
Similar Questions
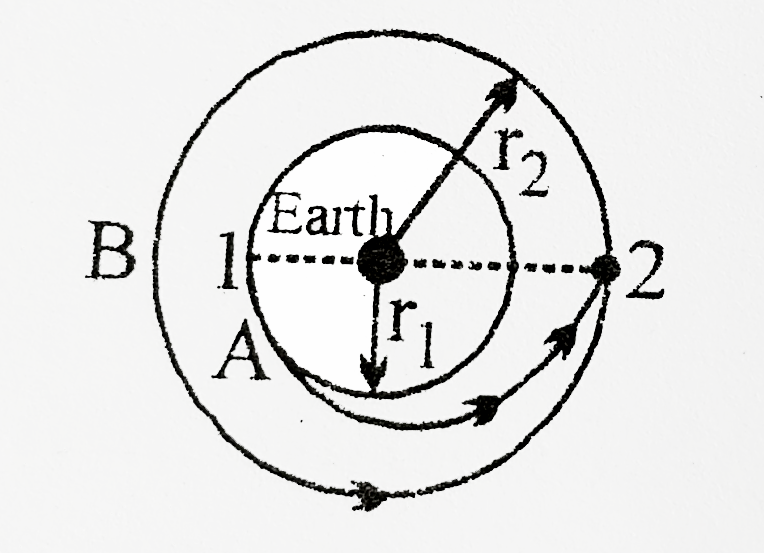
Two satellites A and B are revolving around the earth circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. A?t position 2, A is given another impluse so that velocities of A and B at 2 become equal and the move together.

For any elliptical path of the satellite of the time period of revolution is given by Kepler's planetary law as T2αr3 where a is semi major axis of the ellipse which is r1+r22 in this case. Also angular mopmentum of any satellite revolving around the Earth will remain a constant about EArth's centre as force of gravity on the satellite which keeps it in elliptical path is along its position vector relative to the earth centre.
If the two have same mass
View SolutionTwo satellites A and B are revolving around the earth circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. A?t position 2, A is given another impluse so that velocities of A and B at 2 become equal and the move together.
For any elliptical path of the satellite of the time period of revolution is given by Kepler's planetary law as T2αr3 where a is semi major axis of the ellipse which is r1+r22 in this case. Also angular mopmentum of any satellite revolving around the Earth will remain a constant about EArth's centre as force of gravity on the satellite which keeps it in elliptical path is along its position vector relative to the earth centre.
If r2=3r1 and time period of revolution for B be T than time taken by A in moving from position 1 to position 2
View Solution
Knowledge Check
Three planets revolve round the Sun once in 200, 250 and 300 days, respectively in their own orbits. When do they all come relatively to the same position as at a certain point of time in their orbits ?
AAfter 3000 daysBAfter 2000 daysCAfter 1500 daysDAfter 1200 daysA planet revolves round the sun in an elliptical orbit of semi minor and semi major axes x and y respectively. Then the time period of revolution is proportional to
A(x+y)32B(y−x)32Cx32Dy32A planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
A|v×r|B2|r×v|C∣∣∣12(r×v)∣∣∣DNone of these
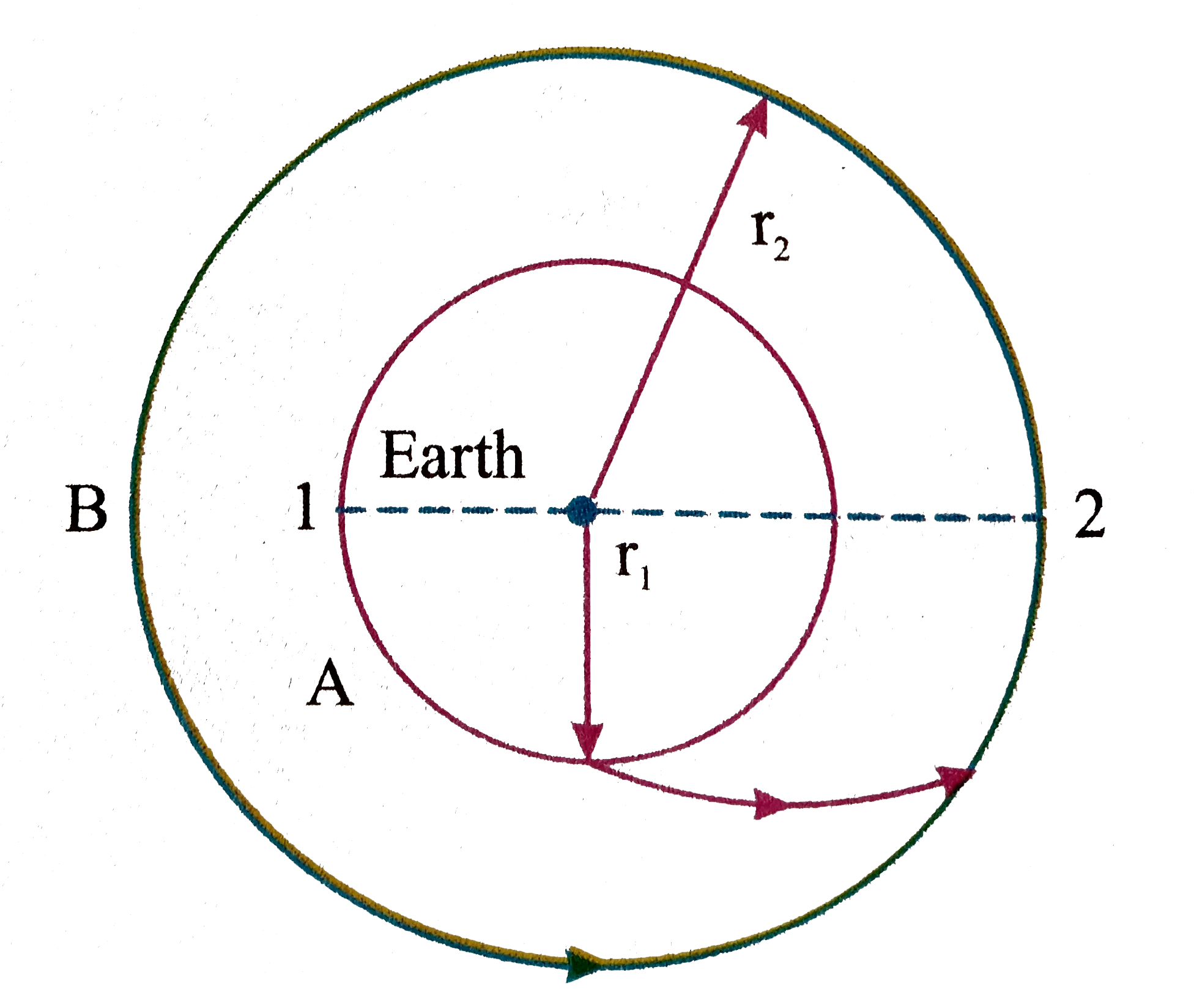
Two satellites A and B are revolving around the earth in circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. focal lengths of the elliptical path are r1 and r2 respectively. at position 2, A is given another impulse so that velocities of A and B at 2 become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as T2αr3 where a is semi-major axis of the ellipse which is r1+r22 in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
When A is given its first impulse at that moment
View Solution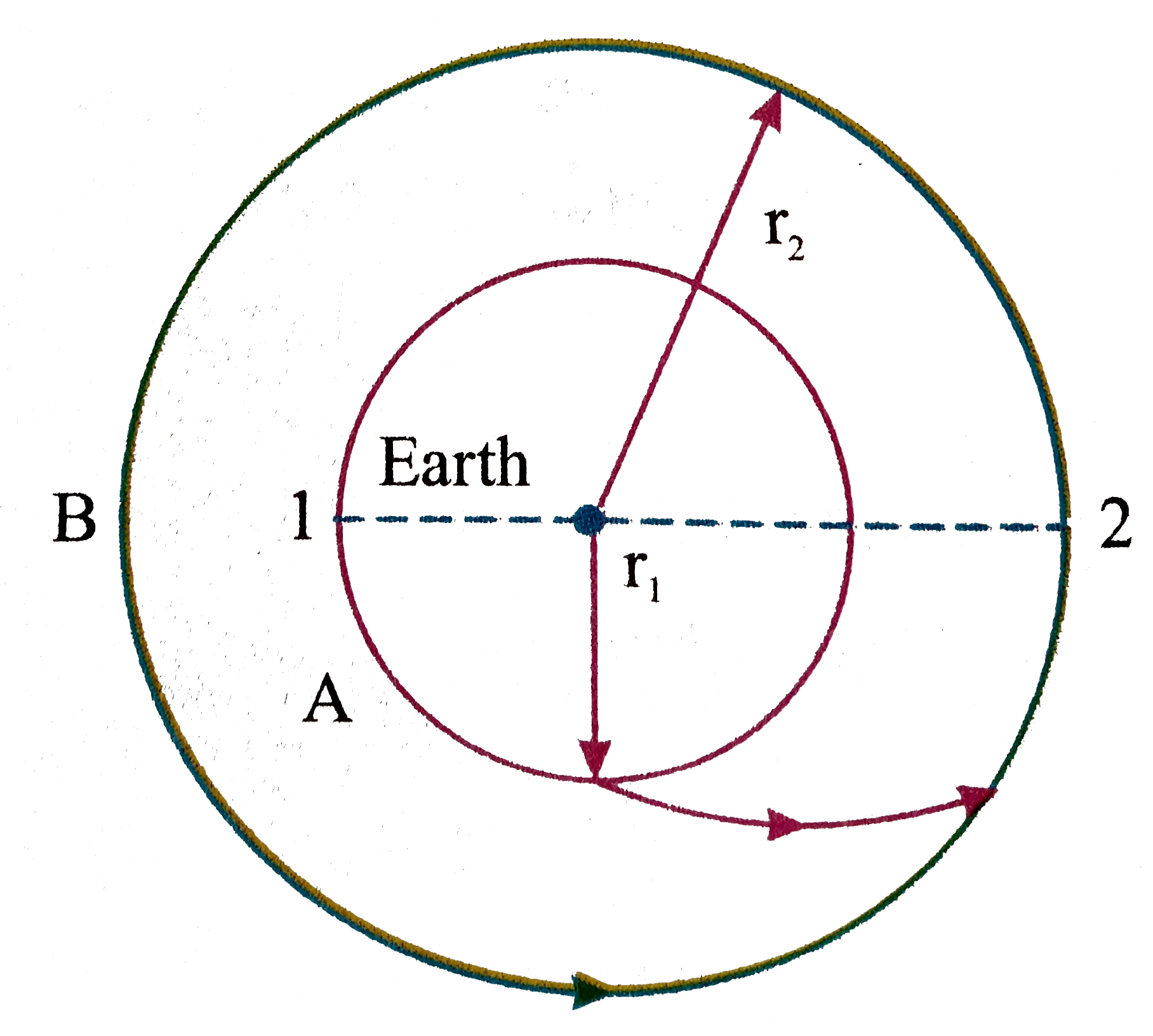
Two satellites A and B are revolving around the earth in circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. focal lengths of the elliptical path are r1 and r2 respectively. at position 2, A is given another impulse so that velocities of A and B at 2 become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as T2αr3 where a is semi-major axis of the ellipse which is r1+r22 in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
If the two have same mass
View SolutionTwo satellites A and B are revolving around the earth circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. A?t position 2, A is given another impluse so that velocities of A and B at 2 become equal and the move together.

For any elliptical path of the satellite of the time period of revolution is given by Kepler's planetary law as T2αr3 where a is semi major axis of the ellipse which is r1+r22 in this case. Also angular mopmentum of any satellite revolving around the Earth will remain a constant about EArth's centre as force of gravity on the satellite which keeps it in elliptical path is along its position vector relative to the earth centre.
When A is given its first impulse at the moment.
View SolutionA planet of mass m is revolving round the sun (of mass Ms) in an elliptical orbit. If →v is the velocity of the planet when its position vector from the sun is →r, then areal velocity of the positon vector of the planet is :
View SolutionA planet goes round the sun three times as fast as the earth. If rpandre are the radii of orbit of the planet and the earth respectively then
View Solution
