Question

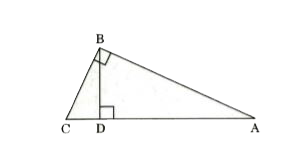
In a triangle ABC, $\angle BCA={90}^{\circ }$ and CD is perpendicular to AB. If AD = 4 cm and BD = 9 cm, then the value of DC will be

Options

A. `sqrt(18) cm`
B. `sqrt(20) cm`
C. `sqrt(65) cm`
D. 6 cm

Explanation

To solve the problem, we will use the properties of right triangles and the relationships between the segments created by the perpendicular line CD.

1. Identify the Triangle and Given Values:
We have triangle ABC where angle BCA = 90 degrees. We are given that AD = 4 cm and BD = 9 cm.

2. Calculate the Length of AB:
Since AD and BD are parts of the segment AB, we can find AB by adding AD and BD together.
\( AB = AD + BD = 4 \, \text{cm} + 9 \, \text{cm} = 13 \, \text{cm} \)

3. Use the Right Triangle Relationships:
In triangle ABC, since CD is perpendicular to AB, we can use the following theorem:
\( CD^2 = AD \times BD \)

4. Substitute the Values:
Now, substitute the values of AD and BD into the equation:
\( CD^2 = 4 \, \text{cm} \times 9 \, \text{cm} = 36 \, \text{cm}^2 \)

5. Calculate the Length of DC:
To find CD, take the square root of both sides:
\( CD = \sqrt{36 \, \text{cm}^2} = 6 \, \text{cm} \)

Thus, the value of DC is 6 cm.