In the figure given below, ABC is a triangle with AB = BC and D is an interior point of the triangle ABC such that ∠DAC=∠DCA.

Consider the following statements :
1. Triangle ADC is an isosceles triangle.
2. Dis the centroid of the triangle ABC.
3. Triangle ABD is congruent to the triangle CBD.
Which of the above statements are correct ?
1 and 2 only
2 and 3 only
1 and 3 only
1, 2 and 3
Step by step video & image solution for In the figure given below, ABC is a triangle with AB = BC and D is an interior point of the triangle ABC such that angle DAC = angleDCA. Consider the following statements : 1. Triangle ADC is an isosceles triangle. 2. Dis the centroid of the triangle ABC. 3. Triangle ABD is congruent to the triangle CBD. Which of the above statements are correct ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In the figure, ABC is a triangle. Measure of ΔABD, (in degrees) is
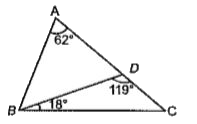 A72B80C57D61
A72B80C57D61In an isosceles triangle ABC base AB=6 cm and each lateral side is 5 cm. find the circumradius of the triangle ABC.
AA)227cmBB)258cmCC)218cmDD)237cm
The centroid of a triangle ABC is G. The area of triangle ABC is 60 cm2. The area of triangle GBC is.
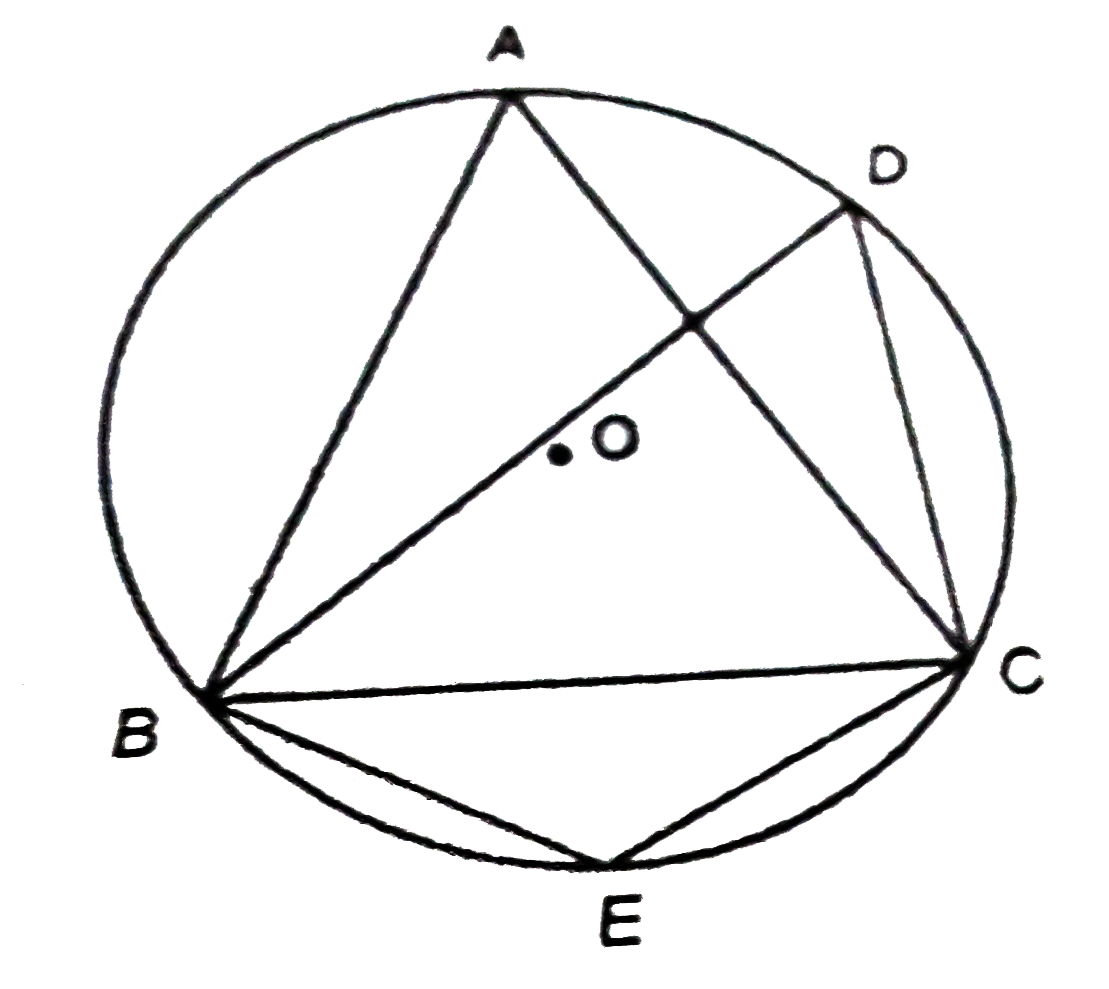
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle. Find the value of ∠BDC and ∠BEC.
View Solution△ABC is an isosceles triangle with AC = BC. If AB2=2AC2 . Prove that △ABC is a right triangle.
View SolutionConsider the following statements :
1. Let D be a point on the side BC of a triangle ABC: If area of triangle ABD = area of triangle ACD, then for all points O on AD, area of triangle ABO = area of triangle ACO.
2. If G is the point of concurrence of the medians of a triangle ABC, then area of triangle ABG = area of triangle BCO = area of triangle ACG.
Which of the above statements is/are correct?
View SolutionConstruct any △ABC. Construct △A'BC' such that AB:A'B=5:3 and △ABC~△A'BC'.
View SolutionABC is an isosceles triangle with AC = BC. If AB2−2AC2=0, prove that ABC is right triangle.
View Solution

