In a circle of radius 5cm, AB and AC are two chords such that AB=AC=8 cm. What is the length of chord BC?
A)9cm
B)9.2 cm
C)9.6 cm
D)9.8 cm
Step by step video & image solution for In a circle of radius 5cm, AB and AC are two chords such that AB=AC=8 cm. What is the length of chord BC? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
There is a circle of radius 5 cm. There are two chords AB and AC OF equal length = 6 cm . Find the length of chord BC .
A4.8 cmB10.8cmC9.6 cmDnone of theseIn the given figure, O is the centre of a circle of radius 13 cm and AB is a chord perpendicular to OD. If CD = 8 cm, then what is the length (in cm) of AB?
 AA)6 cmBB)12 cmCC)24 cmDD)28cm
AA)6 cmBB)12 cmCC)24 cmDD)28cm
In a circle of radius 5cm, AB and AC are two chords such that AB=AC=6cm. The length of chord BC=
(A) 4.8cm
(B) 9.6cm
(C) 2.4cm
(D) 5cm
View SolutionIn a circle of radius 5 cm, AB and Ac are two chords of 6cm each. Find the length of the chord BC.
View SolutionThere is a circle of radius 5 cm. There are two chords AB and AC OF equal length = 6 cm . Find the length of chord BC .
View SolutionIn a circle of radius 13 cm, AB and CD are two equal and chords of lengths 24 cm each .What is the distance between the chords ?
View SolutionIn a circle of radius 5 cm, AB and CD are two parallel chords of lengths 8 cm and 6 cm respectively. Calculate the distance between the chords if they are
(i) on the same side of the centre.
(ii) on the opposite sides of the centre.
View SolutionThe radius of a circle is 10 cm and the perpendicular form the centre to a chord is 8cm. Find the length of the chord.
(ii) The radius of a circle is 10 cm. its one chord is 16 cm long. Find the perpendicular distance of this chord form the centre.
(iii) in the adjoining figure O is the centre of circle. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
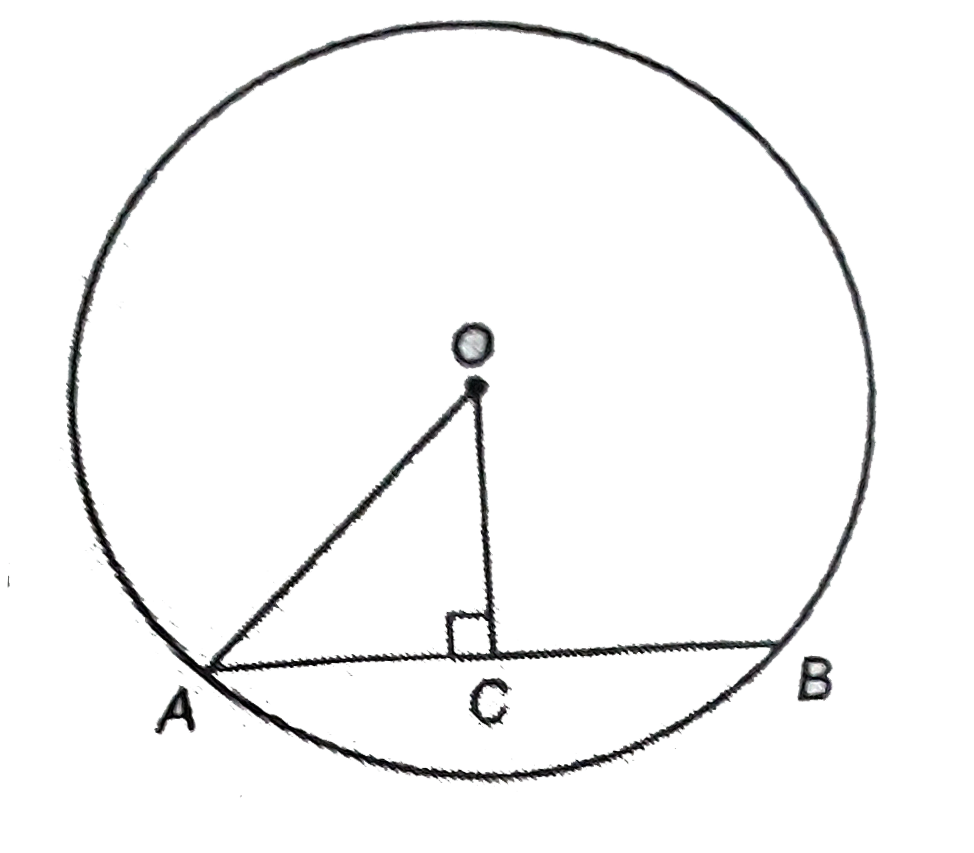
(iv) In the adjoining figure, OM⊥AB, radius OC=5cm and chord AB=8cm.Find the length of OM.
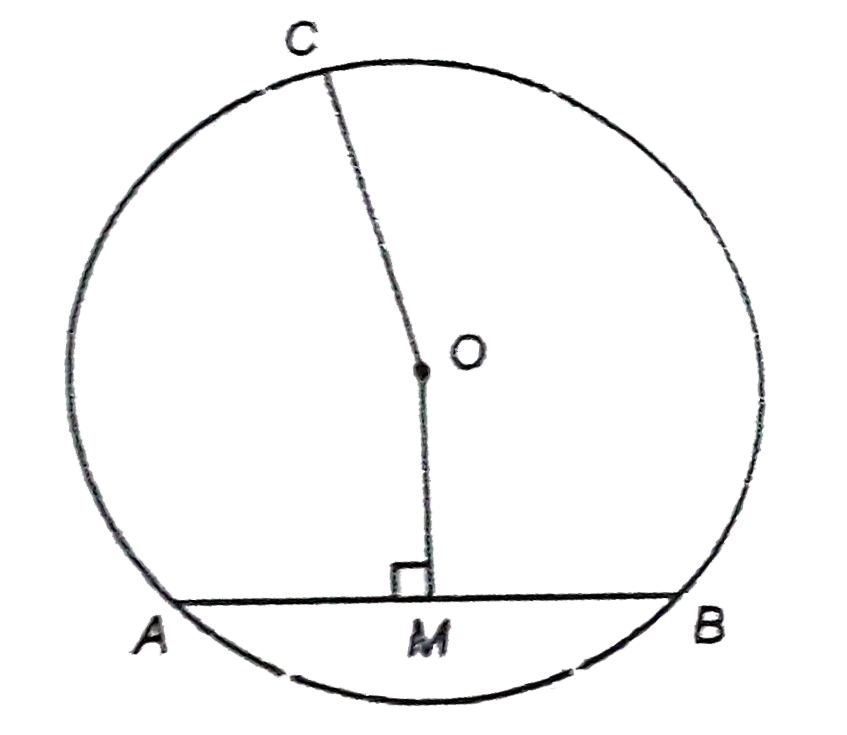
View Solution
