A ladder 5m long is placed in a room so as to reach a point 4.8 m high on a wall and on turning the ladder over to the opposite side of the wall without moving the base, it reaches a point 1.4 m. What is the breadth of the room?
5.8 m
6m
6.2 m
7.5m
To solve the problem step by step, we will use the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Step 1: Identify the lengths and set up the problem
We have a ladder that is 5 meters long. When the ladder is leaned against one wall, it reaches a height of 4.8 meters. When turned to the opposite side, it reaches a height of 1.4 meters. We need to find the breadth of the room, which is the distance between the two walls.
Step 2: Set up the equations using the Pythagorean theorem
Let:
- x = distance from the base of the ladder to the wall where it reaches 4.8 m
- y = distance from the base of the ladder to the wall where it reaches 1.4 m
From the first position of the ladder:
x2+4.82=52
From the second position of the ladder:
y2+1.42=52
Step 3: Calculate x
Substituting the values into the first equation:
x2+4.82=25
Calculating 4.82:
4.82=23.04
Now substituting back:
x2+23.04=25
Subtracting 23.04 from both sides:
x2=25−23.04=1.96
Taking the square root:
x=√1.96=1.4 m
Step 4: Calculate y
Now, substituting the values into the second equation:
y2+1.42=25
Calculating 1.42:
1.42=1.96
Now substituting back:
y2+1.96=25
Subtracting 1.96 from both sides:
y2=25−1.96=23.04
Taking the square root:
y=√23.04=4.8 m
Step 5: Find the breadth of the room
The breadth of the room is the sum of x and y:
Breadth=x+y=1.4+4.8=6.2 m
Final Answer
The breadth of the room is 6.2 meters.
We have a ladder that is 5 meters long. When the ladder is leaned against one wall, it reaches a height of 4.8 meters. When turned to the opposite side, it reaches a height of 1.4 meters. We need to find the breadth of the room, which is the distance between the two walls.
Let:
- x = distance from the base of the ladder to the wall where it reaches 4.8 m
- y = distance from the base of the ladder to the wall where it reaches 1.4 m
x2+4.82=52
From the second position of the ladder:
y2+1.42=52
Substituting the values into the first equation:
x2+4.82=25
Calculating 4.82:
4.82=23.04
Now substituting back:
x2+23.04=25
Subtracting 23.04 from both sides:
x2=25−23.04=1.96
Taking the square root:
x=√1.96=1.4 m
Now, substituting the values into the second equation:
y2+1.42=25
Calculating 1.42:
1.42=1.96
Now substituting back:
y2+1.96=25
Subtracting 1.96 from both sides:
y2=25−1.96=23.04
Taking the square root:
y=√23.04=4.8 m
The breadth of the room is the sum of x and y:
Breadth=x+y=1.4+4.8=6.2 m
The breadth of the room is 6.2 meters.
Similar Questions
A 15-m long ladder is placed against a wall to reach a window 12 m high.Find the distance of the ladder from the wall.
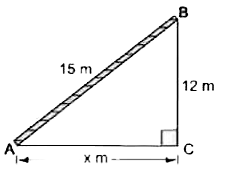 View Solution
View SolutionWalls of two buildings on eiterh side of a street are parallel to each other. A ladder 5.8m long is placed on the street such that its top jist reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
View Solution
Knowledge Check
- Question 1 - Select One
The perimeter of the floor of a room is 18 m and its height is 3 m. What is the area of 4 walls of the room?
A21m2B42m2C54m2D108m2
Walls of two buildings on either side of a street are parallel to each othe. A ladder 5.8m long is placed on the street such that its top just reaches the window of a building at the height of 4m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2m. Find the width of the street.
View SolutionA ladder 20 m long is placed against a wall so that the foot of the ladder is 10 m from the wall. The angle of inclination of the ladder to the horizontal will be :
View SolutionA ladder 3.7 m long is placed against a wall in such a way that the foot of the ladder is 1.2 m away from the wall. Find the height of the wall to which the ladder reaches.
View SolutionA ladder 13 m long reaches a window which is 12 m above the ground on side of a street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 5m high, then the width of the street is:
View SolutionA ladder 50 dm long when set against the wall of a house just reaches a window at a height of 48 dm. How far is the lower end of the ladder from the base of the wall?
View SolutionA ladder of 17 ft. length reaches a window which is 15 ft. above the ground on one side of the street. Keeping its foot at the same point the ladder is turned to the other side of the street and now it reaches a window 8 ft. high. What is the width of the street ?
View SolutionA ladder 10m long rests against a vertical wall. If the foot of the ladder is 6m away from the wall and the ladder just reaches the top of the wall, how high is the wall?
View Solution

