What is the remainder when we divide 450+750 by 65 ?
1
2
0
3
The correct Answer is:C
To find the remainder when 450+750 is divided by 65, we can use properties of modular arithmetic. Here’s a step-by-step solution:
Step 1: Rewrite the expression
We start with the expression:
450+750
Step 2: Use properties of exponents
Notice that both 4 and 7 can be expressed in terms of their squares:
450=(42)25=1625
750=(72)25=4925
So we can rewrite the expression as:
1625+4925
Step 3: Use the sum of powers theorem
According to the theorem, if n is odd, then:
an+bn≡0mod(a+b)
In our case, n=25 (which is odd), a=16, and b=49. Therefore:
1625+4925≡0mod(16+49)
Calculating 16+49:
16+49=65
This means:
1625+4925≡0mod65
Step 4: Conclusion
Since 450+750≡0mod65, the remainder when 450+750 is divided by 65 is:
0
We start with the expression:
450+750
Notice that both 4 and 7 can be expressed in terms of their squares:
450=(42)25=1625
750=(72)25=4925
So we can rewrite the expression as:
1625+4925
According to the theorem, if n is odd, then:
an+bn≡0mod(a+b)
In our case, n=25 (which is odd), a=16, and b=49. Therefore:
1625+4925≡0mod(16+49)
Calculating 16+49:
16+49=65
This means:
1625+4925≡0mod65
Since 450+750≡0mod65, the remainder when 450+750 is divided by 65 is:
0
Topper's Solved these Questions
- SSC SELECTION POST 14 DEC 2020 SHIFT 3 GRADUATION POST BOOK - SSC SELECTION POSTCHAPTER - SSC SELECTION POST 14 DEC 2020 SHIFT 3 GRADUATION POST EXERCISE - QUANTITATIVE APTITUDE
25 Videos
- SSC SELECTION POST 9 NOV 2020 SHIFT 3 GRADUATION LEVELBOOK - SSC SELECTION POSTCHAPTER - SSC SELECTION POST 9 NOV 2020 SHIFT 3 GRADUATION LEVELEXERCISE - QUANTITATIVE APTITUDE
25 Videos
Similar Questions
Knowledge Check
What is the remainder when we divide 570+770 by 74? जब हम 570+770 में 74 से भाग देते ह, तो शेषफल क्या आएगा ?
A0B1C5D7What is the remainder when 41000 is divided by 7 ?
A1B4C2D6
Remainder when
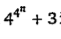 is divided by 7 is:
is divided by 7 is:
View SolutionWhen n is divided by 4, the remainder is 3. What is the remainder when 2n is divided by 4? 1 (b) 2 (c) 3 (d) 6
View SolutionWhat is the remainder when 41000 is divided by 7?
View SolutionWhat is the remainder when 41012 is divided by 7 ?
View SolutionWhat is the remainder when 22010 is divided by 7 ?
View SolutionWhat is the remainder when 22012 is divided by 7 ?
View Solution
