Relation between r.m.s. voltage and instantaneous voltage of an AC
V0=VRMS/√2
VRMS=V0/√2
VRMS=0.70V0
Both (C) and (D)
The correct Answer is:D
To find the relation between the root mean square (RMS) voltage and the instantaneous voltage of an alternating current (AC), we can follow these steps:
Step 1: Understand the Definitions
- Instantaneous Voltage (V): This is the voltage at any given moment in time during the AC cycle. It can be represented as:
V(t)=V0sin(ωt+ϕ)
where V0 is the peak (maximum) voltage, ω is the angular frequency, t is time, and ϕ is the phase angle.
- RMS Voltage (V_rms): This is a measure of the effective value of the AC voltage. It is defined as the square root of the average of the squares of the instantaneous voltages over one complete cycle.
Step 2: Calculate RMS Voltage
The RMS voltage can be calculated using the formula:
Vrms=√1T∫T0(V(t))2dt
where T is the time period of one complete cycle.
Step 3: Substitute the Instantaneous Voltage
Substituting the expression for V(t):
Vrms=√1T∫T0(V0sin(ωt+ϕ))2dt
Step 4: Simplify the Integral
Using the identity sin2(x)=1−cos(2x)2:
Vrms=√V20T∫T01−cos(2(ωt+ϕ))2dt
Step 5: Evaluate the Integral
The integral of cos(2(ωt+ϕ)) over one complete cycle is zero, so:
Vrms=√V20T⋅T2=√V202=V0√2
Step 6: Final Relation
Thus, we arrive at the final relation:
Vrms=V0√2≈0.707V0
Conclusion
The relation between RMS voltage and peak voltage is:
- Vrms=V0√2 or approximately Vrms≈0.707V0.
- Instantaneous Voltage (V): This is the voltage at any given moment in time during the AC cycle. It can be represented as:
V(t)=V0sin(ωt+ϕ)
where V0 is the peak (maximum) voltage, ω is the angular frequency, t is time, and ϕ is the phase angle.
The RMS voltage can be calculated using the formula:
Vrms=√1T∫T0(V(t))2dt
where T is the time period of one complete cycle.
Substituting the expression for V(t):
Vrms=√1T∫T0(V0sin(ωt+ϕ))2dt
Using the identity sin2(x)=1−cos(2x)2:
Vrms=√V20T∫T01−cos(2(ωt+ϕ))2dt
The integral of cos(2(ωt+ϕ)) over one complete cycle is zero, so:
Vrms=√V20T⋅T2=√V202=V0√2
Thus, we arrive at the final relation:
Vrms=V0√2≈0.707V0
The relation between RMS voltage and peak voltage is:
- Vrms=V0√2 or approximately Vrms≈0.707V0.
Similar Questions
Answer the following questions :
(a) In any a.c. circuit, is the applied instantaneous voltage equal to the algebraic sum of the instantaneous voltages acorss the series elements of the circuit ? Is the same true for r.m.s. voltage?
(b) A capacitor is used in the primary circuit of an induction coil.
(c ) An applied voltage signal consists of a superposition of a d.c. voltage and an a.c. voltage of high frequency. The circuit consists of an inductor and a capacitor in series. Show that the d.c. signal will appear across C and the a.c. signal will appear across L.
(d) A choke coil in series with a lamp is connected to a d.c. line. The lamp is seen to shine brightly. Insertion of an iron core in the choke causes no change in the lamp's brightness. Predict the corresponding observation if the connection is to an a.c. line.
(e) Why is choke coil needed in use of fluorescent tubes with ac mains ? Why can we not use an ordinary resistor instead of choke coil?
View SolutionAn inductor (L=2000mH) is connected to an AC source of peak current. What is the instantaneous voltage of the source when the current is at its peak value?
View Solution
Knowledge Check
The r.m.s. voltage of domestic electricity supply is 220 volt. Electrical appliances should be designed to withstand an instantaneous voltage of
A220VB311VC330VD440VPhase difference between voltage and corrent when an ac source is connected to an inductor :
A0∘B90∘C45∘D180∘In an AC series circuit, the instanctaneous current is zero when the instantaneous voltage is xamimum. Connected to the source may be a
Apure inductorBpure capacitorCpure resistorDcombination of an inductor and a capacitor
What will be the instantaneous voltage for a.c. supply of 220 V at 50 hertz ?
View SolutionWhat will be the instantaneous voltage for an a.c. supply of 230 V and 50 Hz?
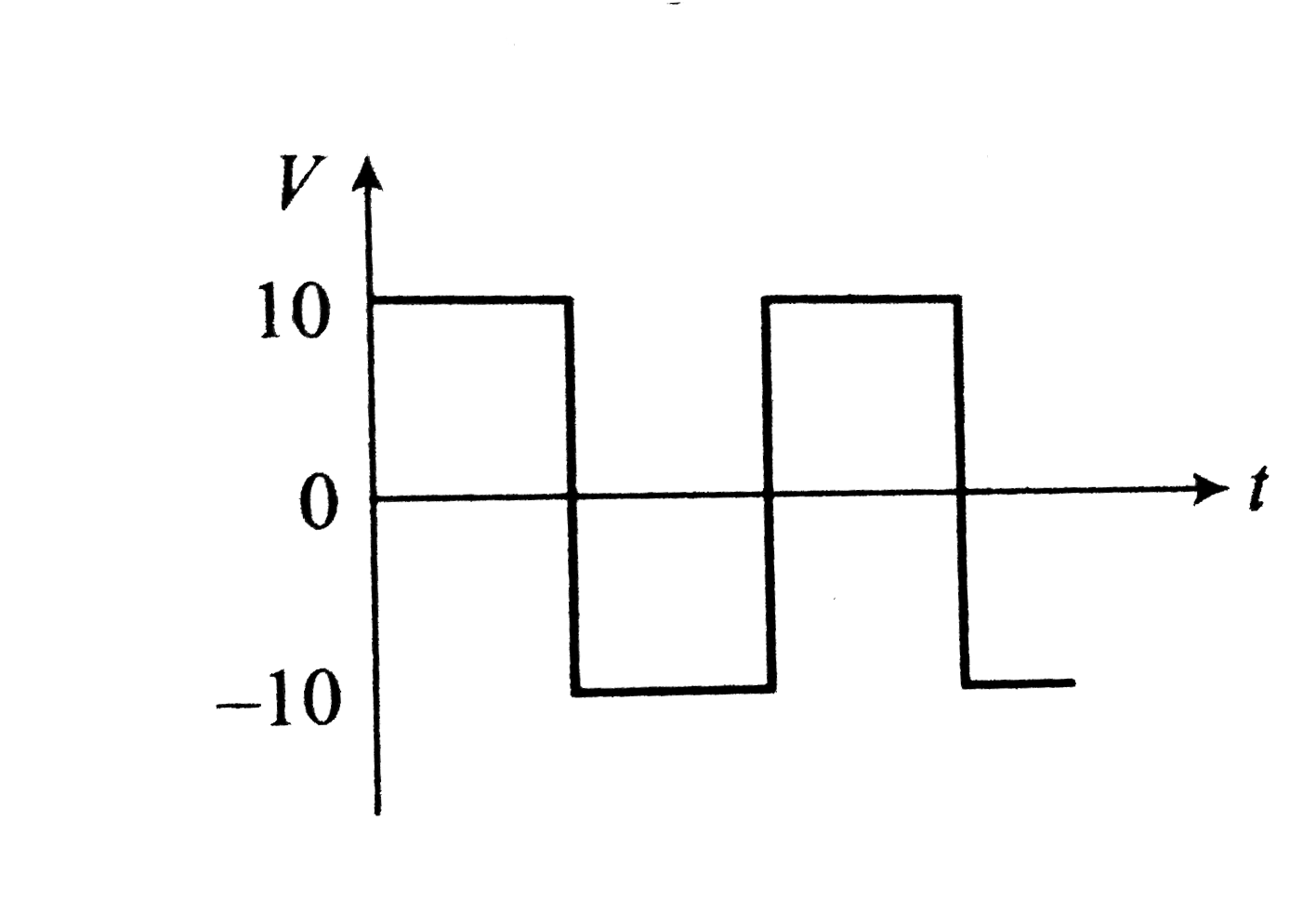
View SolutionThe r.m.s. voltage of the wave form shown is
View SolutionIn an a.c. series circuit, the instantaneous current is maximum when the instantaneous voltage is maximum. The circuit element connected to the source will be
View SolutionIn case of a.c circuit, Ohm's law holds good for
a) Peak values of voltage and current
b) Effective values of voltage and current
c) Instantaneous values of voltage and current
View Solution
