The complex numbers z1=2+5i, z2=3−4i and z3=−4+i are represented by the points A, B and C respectively on an Argand diagram. Sketch the Argand diagram
Video Solution
Text Solution
For z1=2+5t, plot A(2,5)
For z2=3−4i, plot B(3, -4)
For z3=−4+i, plot C(-4, 1)
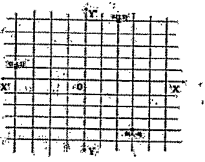
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The points represented by the complex numbers 1+i,−2+3i and 53i on the argand diagram are
Avertices of an equilateral triangleBvertices of an isosceles triangleCcollinearDNone of the above - Question 2 - Select One
The points represented by the complex numbers 1+i,−2+3i and 53i on the argand diagram are
AVertices of an equilateral triangleBVertices of an isosceles triangleCCollinearDNone of the above - Question 3 - Select One
Which of the following represent the complex number z=5-3i on an argand diagram ?
A B
B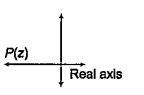 C
C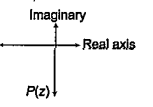 D
D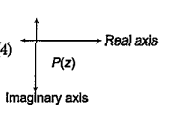
Show that complex numbers z1=−1+5i and z2=−3+2i on the argand plane.
View SolutionThe region represented by inequalities arg(z)≤π3;|z|≤2;Im(z)≥1 in the argand diagram is given by
View SolutionThe points 9+i,4+13i,−8+8i.−3−4i in the Argand diagram represent
View SolutionIf z4=(z−1)4 then the roots are represented in the Argand plane by the points that are
View Solutionif |z+1|=√2|z−1| then the locus described by the point z in the Argand diagram is
View Solution

