Find the product of [ab−ba][a−bba]
To find the product of the matrices (ab−ba) and (a−bba), we will follow the standard procedure for matrix multiplication.
Step 1: Identify the matrices
Let:
A=(ab−ba),B=(a−bba)
Step 2: Set up the multiplication
We want to calculate the product AB:
AB=(ab−ba)(a−bba)
Step 3: Calculate the elements of the resulting matrix
To find the elements of the resulting matrix, we will compute each entry as follows:
1. First row, first column:
(a⋅a)+(b⋅b)=a2+b2
2. First row, second column:
(a⋅−b)+(b⋅a)=−ab+ab=0
3. Second row, first column:
(−b⋅a)+(a⋅b)=−ba+ab=0
4. Second row, second column:
(−b⋅−b)+(a⋅a)=b2+a2
Step 4: Combine the results
Now we can combine these results into the resulting matrix:
AB=(a2+b200a2+b2)
Step 5: Factor out the common term
We can factor out a2+b2:
AB=(a2+b2)(1001)=(a2+b2)I
where I is the identity matrix.
Final Answer
Thus, the product of the two matrices is:
AB=(a2+b2)I
Let:
A=(ab−ba),B=(a−bba)
We want to calculate the product AB:
AB=(ab−ba)(a−bba)
To find the elements of the resulting matrix, we will compute each entry as follows:
(a⋅a)+(b⋅b)=a2+b2
(a⋅−b)+(b⋅a)=−ab+ab=0
(−b⋅a)+(a⋅b)=−ba+ab=0
(−b⋅−b)+(a⋅a)=b2+a2
Now we can combine these results into the resulting matrix:
AB=(a2+b200a2+b2)
We can factor out a2+b2:
AB=(a2+b2)(1001)=(a2+b2)I
where I is the identity matrix.
Thus, the product of the two matrices is:
AB=(a2+b2)I
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the product of (a+b+2c)(a2+b2+4c2−ab−2bc−2ca).
(a+b+2c)(a2+b2+4c2−ab−2bc−2ca) का गुणनफल ज्ञात करें ।Aa3+b3+8c3−abcBa3+b3+8c3−6abcCa3+b3+8c3−2abcDa3+b3+6c3−6abc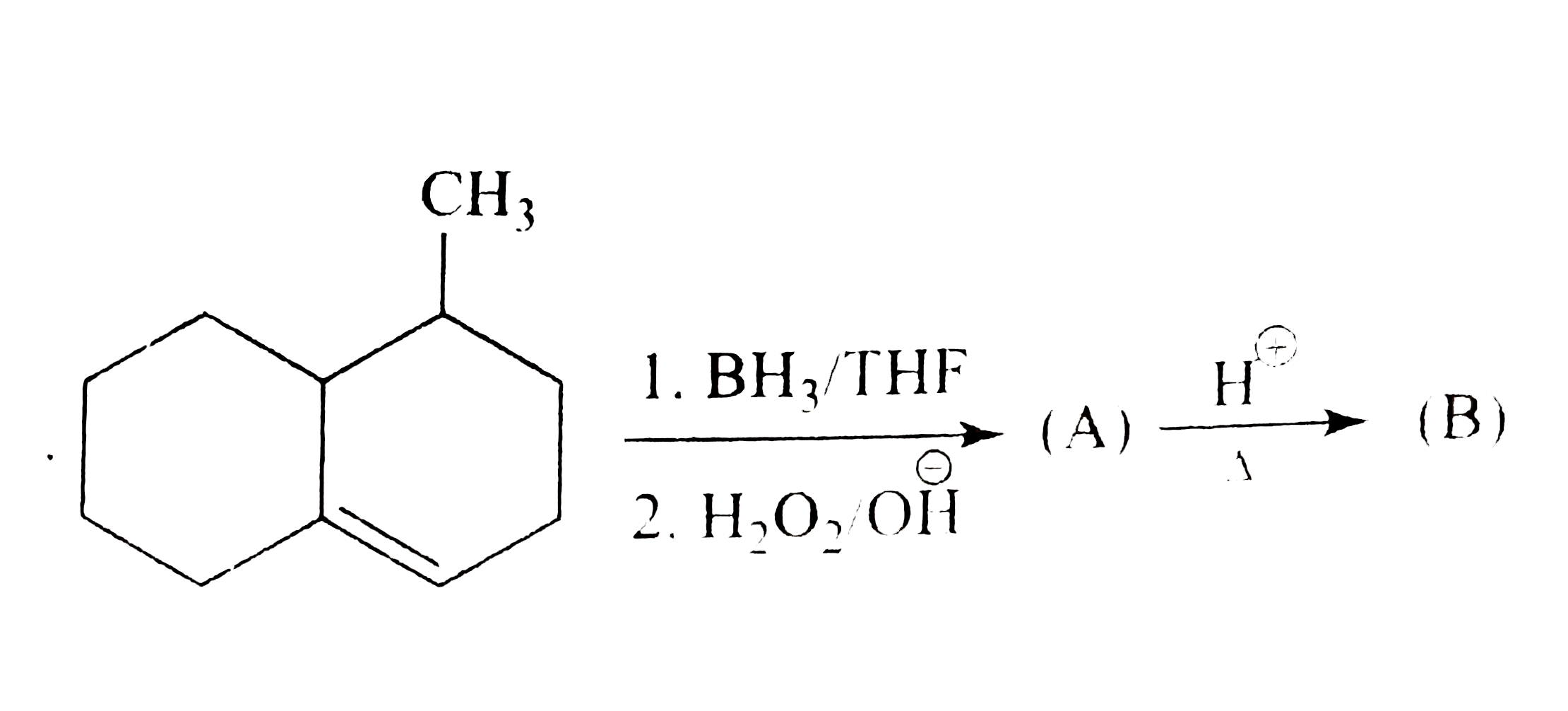 The product (B) is :A
The product (B) is :A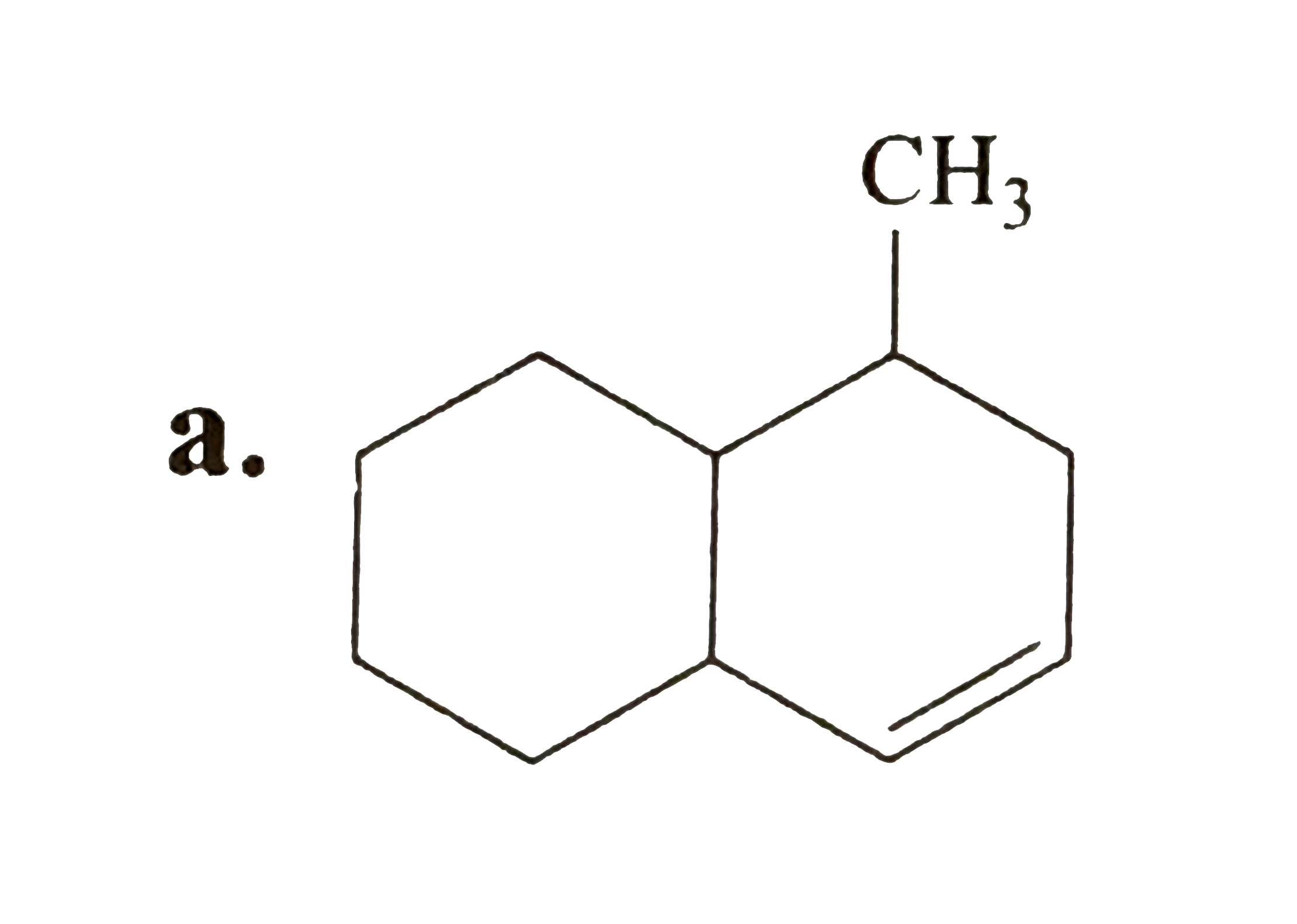 B
B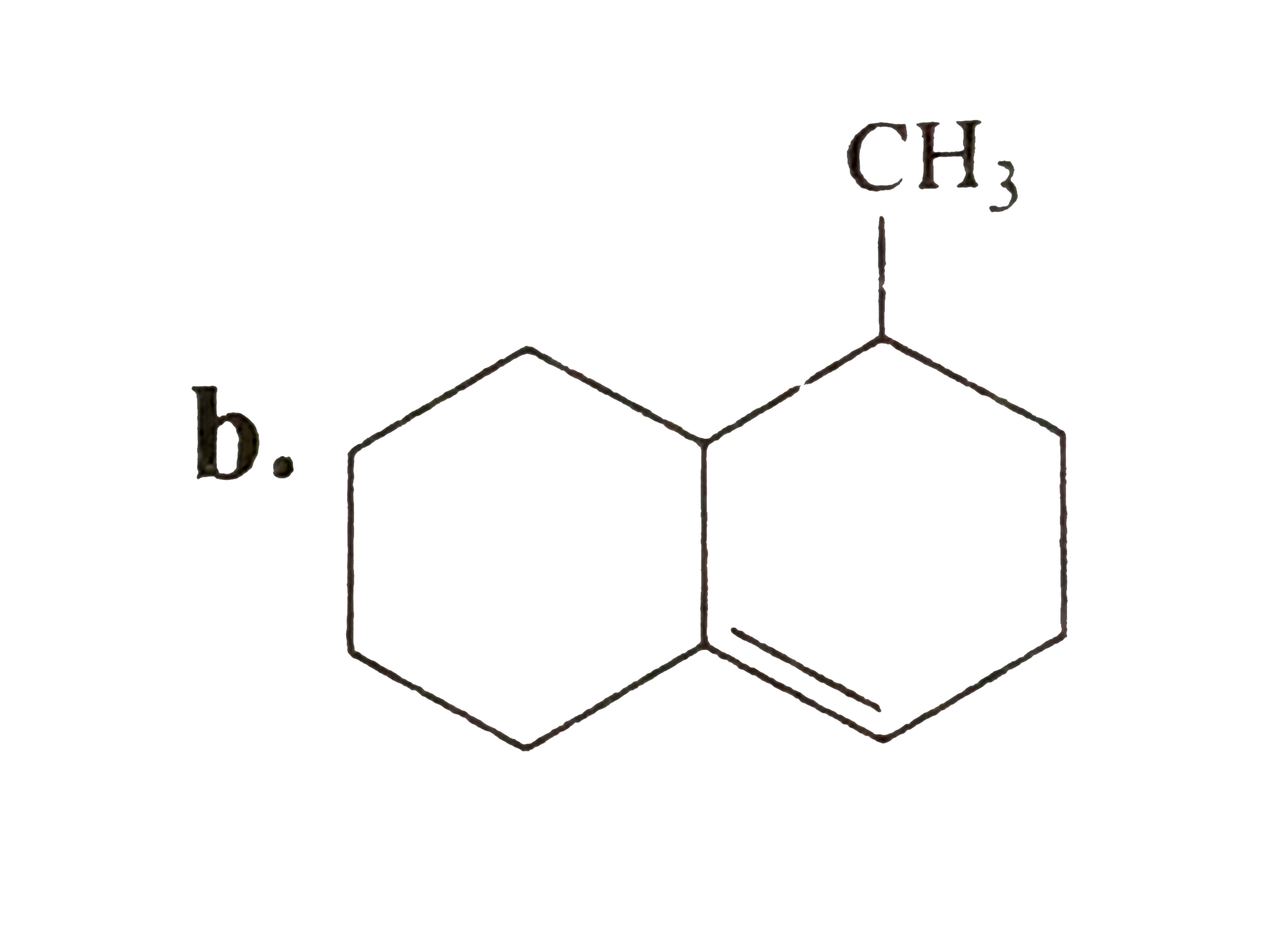 C
C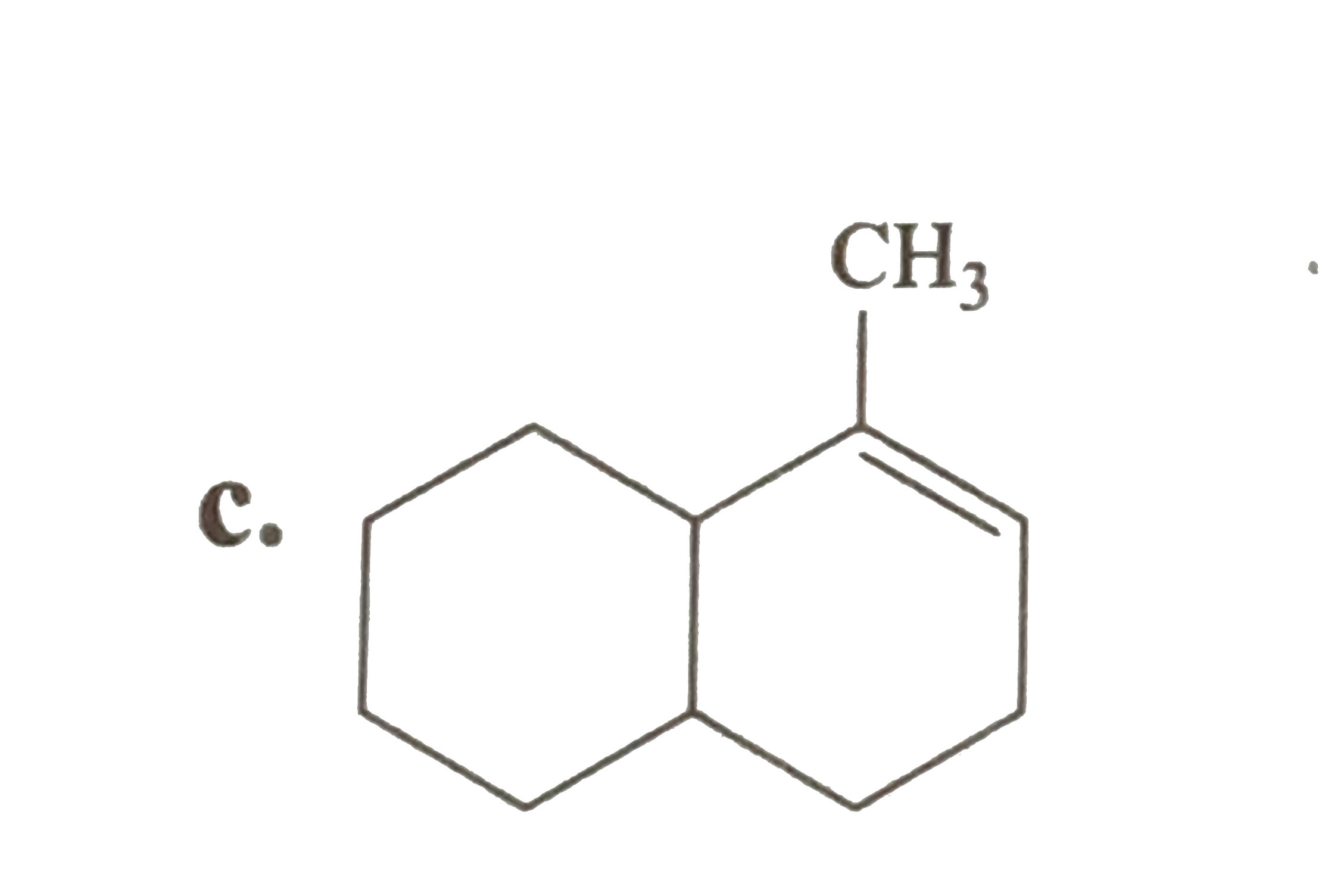 DAll
DAll
Find the product of (a+b+c)[(a−b)2+(b−c)2+(c−a)2].
View SolutionFind the product of (3a + 4b) and (3a - 4b) and verify it when a = -1 and b = 1 .
View SolutionFind the product of (3a + 4b) and (3a - 4b) and verify it when a = -1 and b = 1 .
View SolutionFind the product : (a2+b2)(a4+b4)(a+b)(a−b).
View SolutionFind the products
(2a2b3)×(−3a3b)
View SolutionFind the product (7a−5b)(49a2+35ab+25b2).
View Solution
