The following figure is a right pyramid with an isosceles triangle base. Find the volume of the pyramid if the height is 18 cm

First, we have to calculate the area of the base.
To do that we need to get the height of the isosceles triangle that forms the base.

Using Pythagorean Theorem, x=√132−52=12 cm
Area of triangle = 12×10×13=65cm2
∴ Volume of pyramid=13×65×18=390cm3
Topper's Solved these Questions
Similar Questions
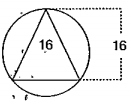
In the following diagram, the height and base of an isosceles triangle are 16 cm each. Find the area of the circumscribing circle.
View SolutionThe base of a right pyramid is an equilateral triangle of side 4cm .The height of the pyramid is half of its slant height. The volume of the pyramid is:
A) 8√39cm3
B)4√39cm3
C)163cm3
D)18√3cm3
View Solution
Knowledge Check
The base of a right pyramid is a square of side 40 cm long. If the volume of the pyramid is 8000cm3, then its height is :
A5 cmB10 cmC15 cmD20 cmThe base area of a right pyramid is 57 sq. units and height is 10 units. Then the volume of the pyramid is
A190 cubic unitsB380 cubic unitsC540 cubic unitsD570 cubic unitsA pyramid is a solid figure whose base is
Aonly a triangleBonly a squareConly a rectangleDany polygon
The base of a right pyramid is an equilateral triangle with side 8 cm, and the height of the pyramid is 24√3 cm. The volume (in cm3) of the pyramid is:
View SolutionThe base of a right prism is a right angled isosceles triangle whose hypotenuse is a cm. If the height of the prism is h cm, then its volume is
View SolutionThe base of a right pyramid is an equilateral triangle of perimeter 8 dm and the height of the pyramid is 30√3 cm. Find the volume of the pyramid.
View SolutionThe base of a right pyramid is an equilateral triangle of side 10√3cm. If the total surface area of the pyramid is 270√3. Sq. cm, its height is
View SolutionBase of a right pyramid is a square whose area is 324 sq metre. If the volume of the pyramid is 1296 cu. metre, then the area (in sq. metre) of the slant surface is
View Solution
