Plot the following polar coordinates:
(3,−π3)
To plot the polar coordinates (3,−π3), we will first convert these polar coordinates into Cartesian coordinates using the formulas for conversion.
1. Identify the Polar Coordinates:
The given polar coordinates are r=3 and θ=−π3.
2. Use the Conversion Formulas:
The formulas to convert polar coordinates (r,θ) to Cartesian coordinates (x,y) are:
x=rcos(θ)
y=rsin(θ)
3. Calculate x:
Substitute r and θ into the formula for x:
x=3cos(−π3)
The cosine function is even, so:
cos(−π3)=cos(π3)=12
Therefore:
x=3⋅12=32
4. Calculate y:
Now substitute r and θ into the formula for y:
y=3sin(−π3)
The sine function is odd, so:
sin(−π3)=−sin(π3)=−√32
Thus:
y=3⋅(−√32)=−3√32
5. Write the Cartesian Coordinates:
The Cartesian coordinates corresponding to the polar coordinates (3,−π3) are:
(32,−3√32)
6. Plot the Point:
On the Cartesian plane, locate the point (32,−3√32). The x-coordinate 32 is approximately 1.5, which is on the positive side of the x-axis. The y-coordinate −3√32 is negative, which means it is below the x-axis.
Final Answer:
The Cartesian coordinates are (32,−3√32).
The given polar coordinates are r=3 and θ=−π3.
The formulas to convert polar coordinates (r,θ) to Cartesian coordinates (x,y) are:
x=rcos(θ)
y=rsin(θ)
Substitute r and θ into the formula for x:
x=3cos(−π3)
The cosine function is even, so:
cos(−π3)=cos(π3)=12
Therefore:
x=3⋅12=32
Now substitute r and θ into the formula for y:
y=3sin(−π3)
The sine function is odd, so:
sin(−π3)=−sin(π3)=−√32
Thus:
y=3⋅(−√32)=−3√32
The Cartesian coordinates corresponding to the polar coordinates (3,−π3) are:
(32,−3√32)
On the Cartesian plane, locate the point (32,−3√32). The x-coordinate 32 is approximately 1.5, which is on the positive side of the x-axis. The y-coordinate −3√32 is negative, which means it is below the x-axis.
The Cartesian coordinates are (32,−3√32).
Topper's Solved these Questions
Similar Questions
Plot the following polar coordinates:
(−3,−3π4)
View SolutionPlot the following polar coordinates:
(3,7π4)
View SolutionPlot the following polar coordinates:
(−2,5π2)
View SolutionConvert the following polar coordinates to its equivalent Cartesian coordinates.
(i) (2,π)
(ii) (√3,π/6)
View SolutionConvert into polar coordinates:
(-3,3)
View SolutionConvert the following points from polar coordinates to the corresponding Cartesian coordinates.
(i) (2,π/3)
(ii) (0.π/2)
(iii) (−√2,π/4)
View SolutionPlot the following points on coordinate plane P(3,1),Q(8,1),R(8,−3),S(3,−3)
View SolutionPlot the following points on the coordinate plane. What do you observe ?
(a) (−2,−3),(−1,−3),(0,−3),(2,−3)
(b) (5,3),(5,2),(5,1),(5,0),(5,−1)
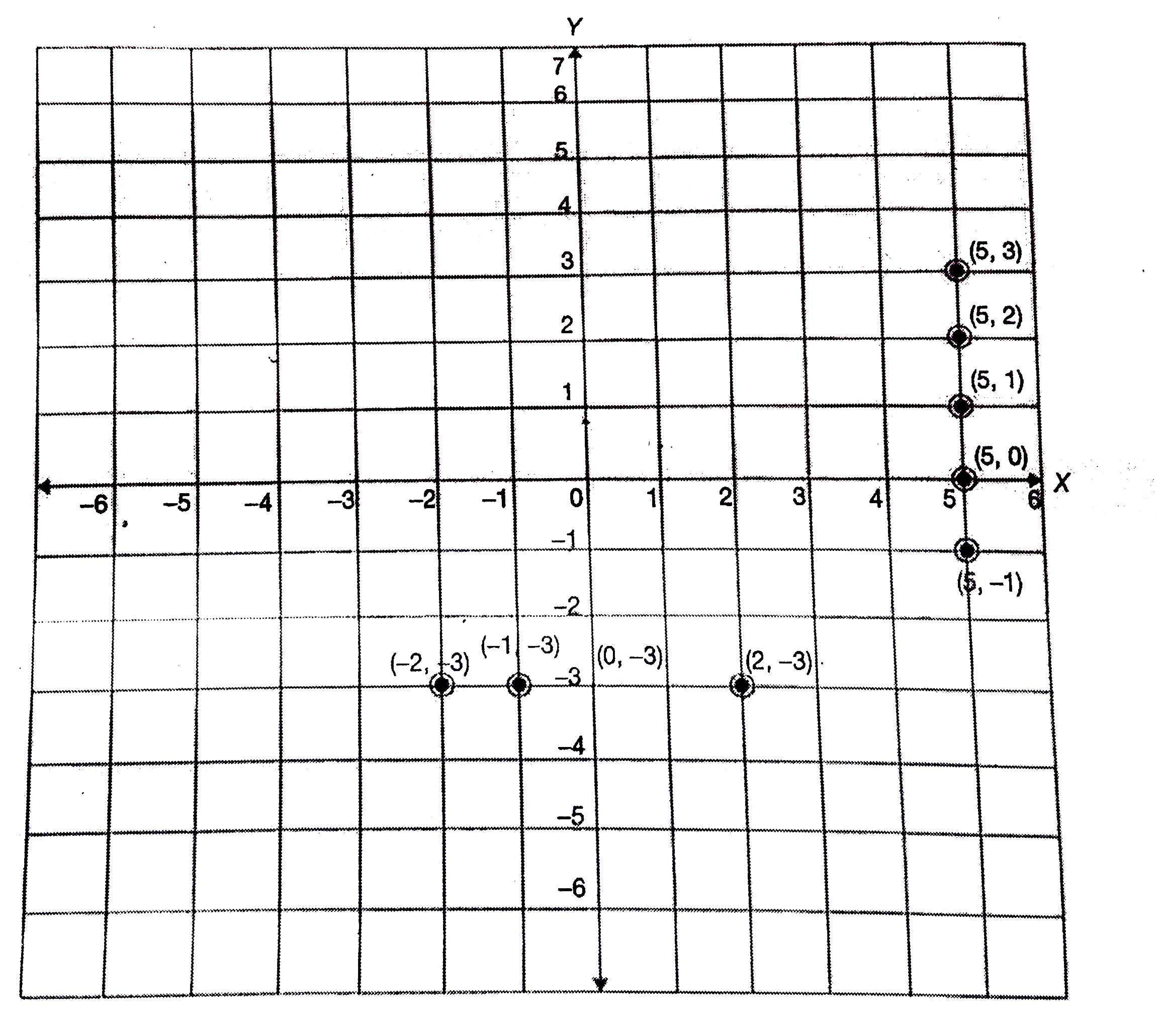
View SolutionPlot the following points on the coordinate plane and what do you obseve ?
(−3,3),(−2,2),(−1,1),(0,0),(1,−1),(2,−2),(3,−3)
View SolutionConvert into polar coordinates:
(0,6)
View Solution
