Question

A man is walking away from the foot of a tower of height 40m at the rate of $4km/hour$.Find the rate at which his distance from the top of the tower is increasing when he is 30m away from the bottom of the tower.

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the Problem
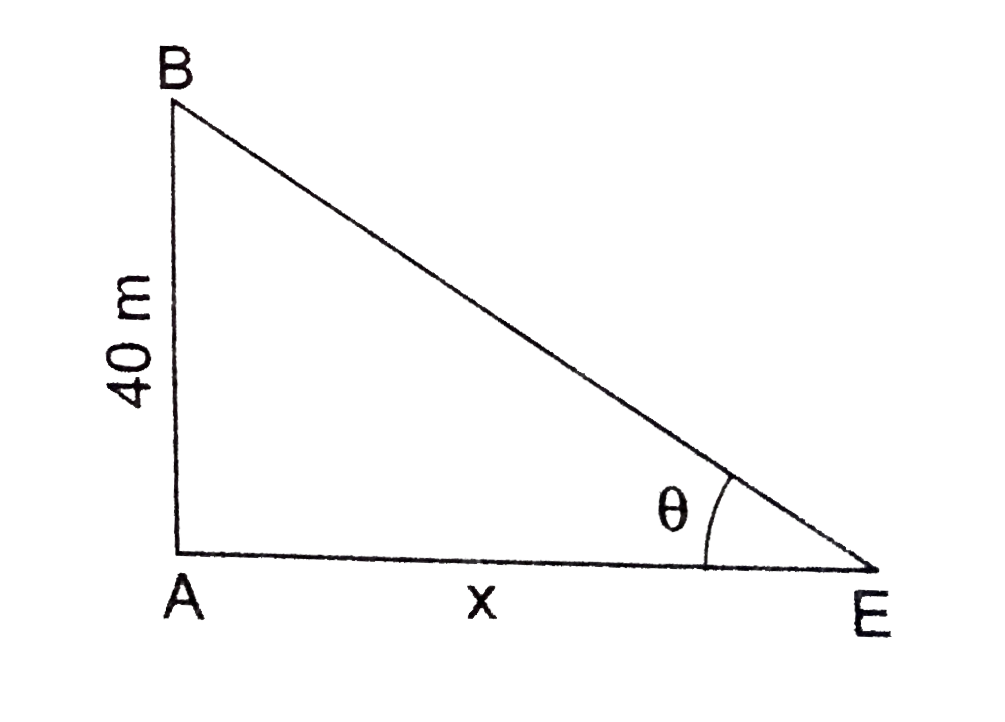
We have a tower of height 40 meters, and a man is walking away from the base of the tower at a rate of 4 km/h. We need to find the rate at which his distance from the top of the tower is increasing when he is 30 meters away from the base of the tower.

Step 2: Set Up the Geometry
Let:
- \( AC \) be the height of the tower = 40 m.
- \( AB \) be the distance from the man to the base of the tower = \( x \) m.
- \( BC \) be the distance from the man to the top of the tower = \( y \) m.

We can form a right triangle \( ABC \) where:
- \( AB = x \)
- \( AC = 40 \)
- \( BC = y \)

Step 3: Apply the Pythagorean Theorem
From the right triangle, we have:
\( y^2 = x^2 + 40^2 \)
This simplifies to:
\( y^2 = x^2 + 1600 \)

Step 4: Differentiate with Respect to Time
Now, we differentiate both sides with respect to time \( t \):
\( \frac{d}{dt}(y^2) = \frac{d}{dt}(x^2 + 1600) \)
Using the chain rule:
\( 2y \frac{dy}{dt} = 2x \frac{dx}{dt} \)

Step 5: Solve for \( \frac{dy}{dt} \)
Rearranging gives:
\( \frac{dy}{dt} = \frac{x}{y} \cdot \frac{dx}{dt} \)

Step 6: Substitute Known Values
We know:
- \( \frac{dx}{dt} = 4 \) km/h (which we need to convert to meters per hour: \( 4 \times 1000 = 4000 \) m/h)
- When the man is 30 m away from the tower, \( x = 30 \) m.

First, we need to find \( y \) when \( x = 30 \):
\( y^2 = 30^2 + 40^2 = 900 + 1600 = 2500 \)
Thus,
\( y = \sqrt{2500} = 50 \text{ m} \)

Step 7: Calculate \( \frac{dy}{dt} \)
Now substituting \( x = 30 \), \( y = 50 \), and \( \frac{dx}{dt} = 4000 \) m/h into the equation:
\( \frac{dy}{dt} = \frac{30}{50} \cdot 4000 = \frac{3}{5} \cdot 4000 = 2400 \text{ m/h} \)

Step 8: Convert to km/h
To convert this to kilometers per hour:
\( \frac{2400}{1000} = 2.4 \text{ km/h} \)

Final Answer
The rate at which the distance from the top of the tower is increasing when the man is 30 m away from the base of the tower is 2.4 km/h.

---