What does the slope of a displacement-tine graph represent? Can displacement-time graph be parallel to the displacement axis? Give reason for your answer.
Step-by-Step Solution:
1. Understanding the Slope of a Displacement-Time Graph:
- The slope of a displacement-time graph represents the velocity of the object.
- Mathematically, slope (m) is defined as the change in displacement (Δy) divided by the change in time (Δx), which can be expressed as:
slope=ΔdisplacementΔtime=y2−y1x2−x1
- Therefore, a steeper slope indicates a higher velocity, while a flatter slope indicates a lower velocity.
2. Can a Displacement-Time Graph be Parallel to the Displacement Axis?:
- A displacement-time graph can be parallel to the displacement axis (the y-axis).
- This scenario occurs when the object is at rest, meaning there is no change in displacement over time.
- In this case, the slope of the graph would be zero, indicating that the velocity is zero.
3. Reasoning for the Answer:
- If the graph is parallel to the displacement axis, it implies that the object is not moving.
- Since the slope is zero, it indicates that there is no change in displacement (Δy = 0) regardless of the change in time (Δx), confirming that the velocity is zero.
Conclusion:
- The slope of a displacement-time graph represents the velocity of the object.
- Yes, a displacement-time graph can be parallel to the displacement axis when the object is at rest, indicating zero velocity.
- The slope of a displacement-time graph represents the velocity of the object.
- Mathematically, slope (m) is defined as the change in displacement (Δy) divided by the change in time (Δx), which can be expressed as:
slope=ΔdisplacementΔtime=y2−y1x2−x1
- Therefore, a steeper slope indicates a higher velocity, while a flatter slope indicates a lower velocity.
- A displacement-time graph can be parallel to the displacement axis (the y-axis).
- This scenario occurs when the object is at rest, meaning there is no change in displacement over time.
- In this case, the slope of the graph would be zero, indicating that the velocity is zero.
- If the graph is parallel to the displacement axis, it implies that the object is not moving.
- Since the slope is zero, it indicates that there is no change in displacement (Δy = 0) regardless of the change in time (Δx), confirming that the velocity is zero.
- The slope of a displacement-time graph represents the velocity of the object.
- Yes, a displacement-time graph can be parallel to the displacement axis when the object is at rest, indicating zero velocity.
Topper's Solved these Questions
- DESCRIPTION OF MOTIONBOOK - CENGAGE PHYSICSCHAPTER - DESCRIPTION OF MOTIONEXERCISE - MANDATORY EXERCISE (EXERCISE SET - III)
12 Videos
- DESCRIPTION OF MOTIONBOOK - CENGAGE PHYSICSCHAPTER - DESCRIPTION OF MOTIONEXERCISE - CONSOLIDATED EXERCISE (COMPREHENSION)
7 Videos
- DESCRIPTION OF MOTIONBOOK - CENGAGE PHYSICSCHAPTER - DESCRIPTION OF MOTIONEXERCISE - MANDATORY EXERCISE (EXERCISE SET - I)
22 Videos
- ELASTICITYBOOK - CENGAGE PHYSICSCHAPTER - ELASTICITYEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
Similar Questions
Knowledge Check
Which of the following displacement-time graphs represent damped harmonic oscillation?
A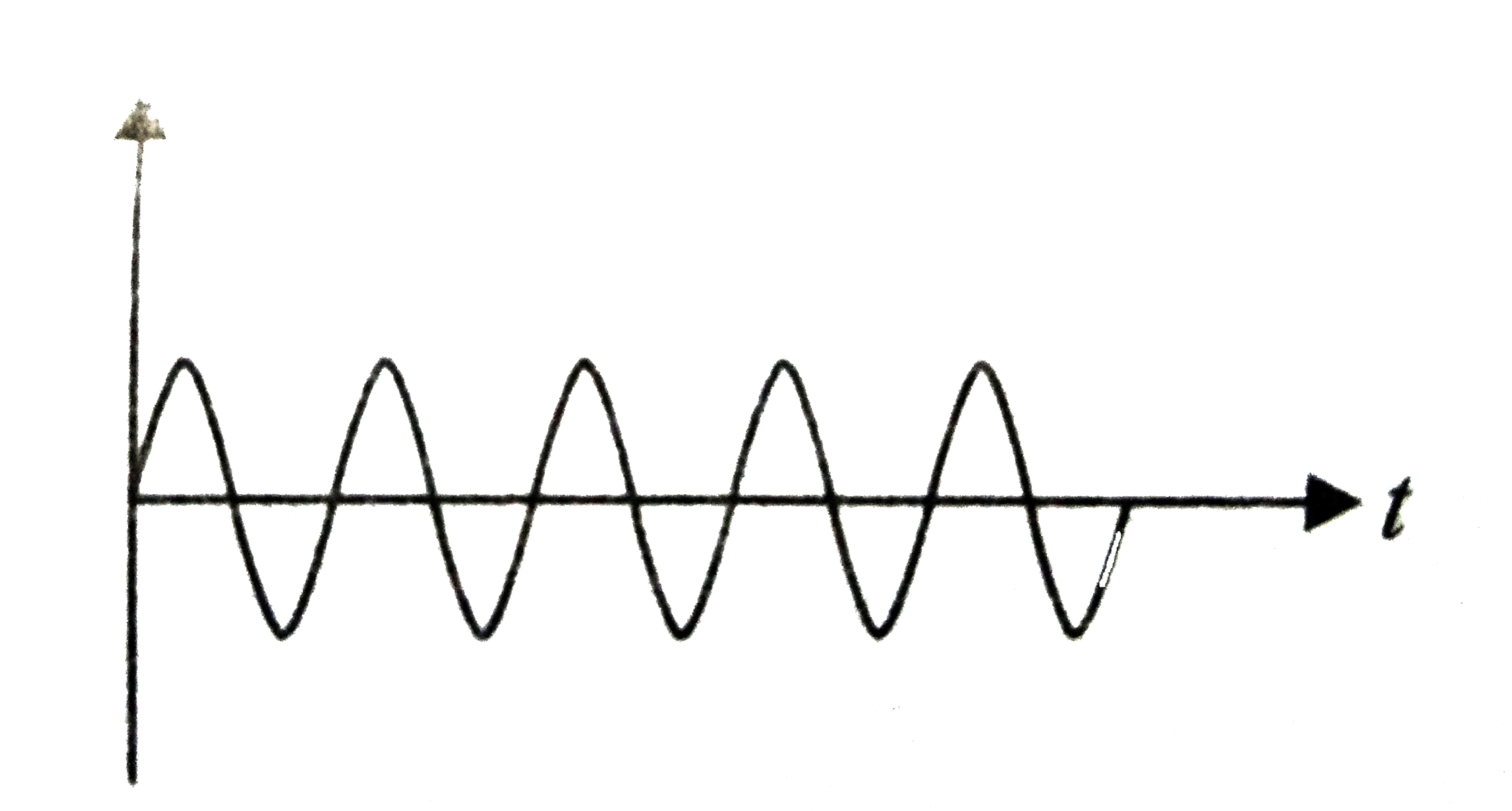 B
B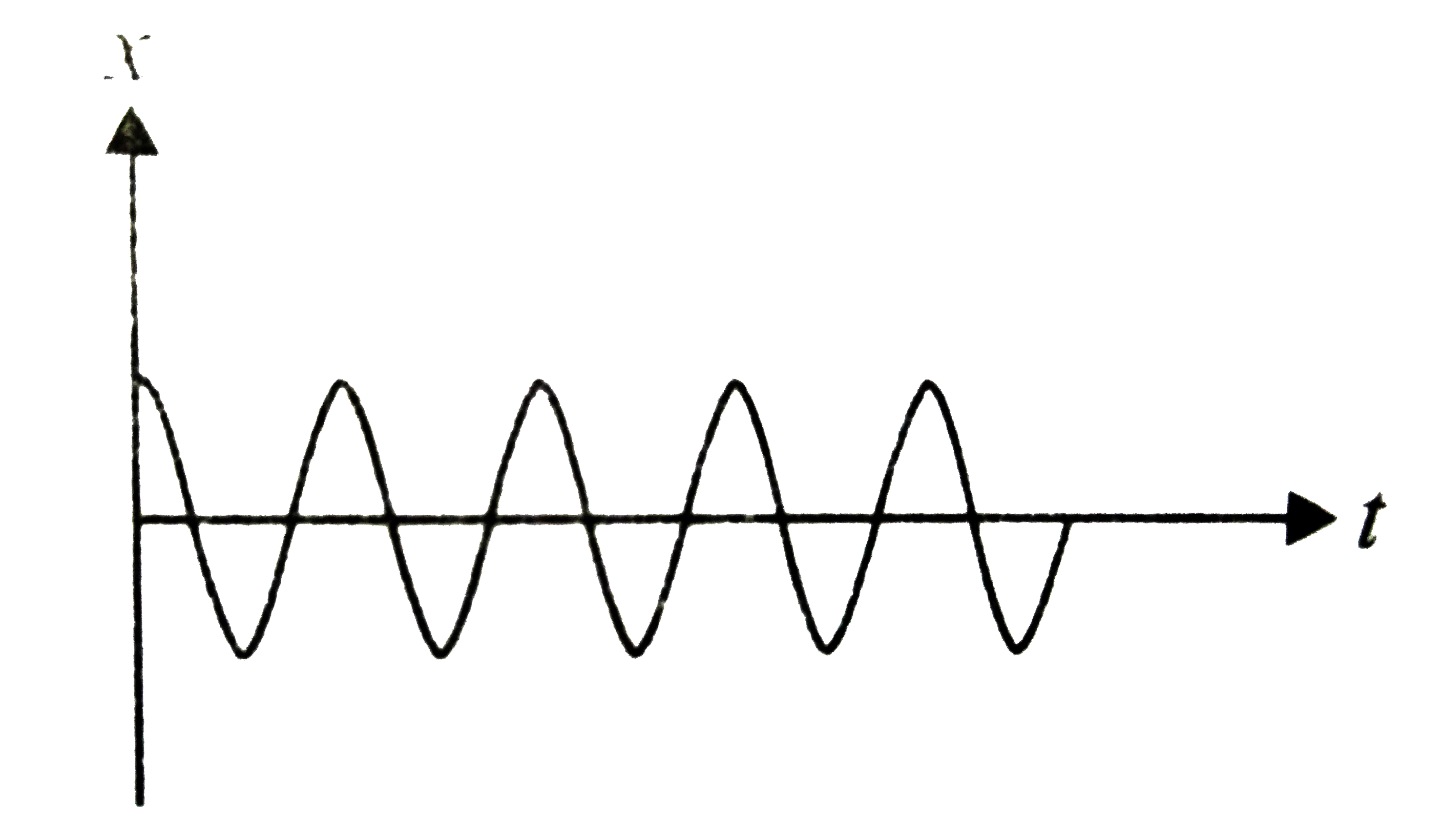 C
C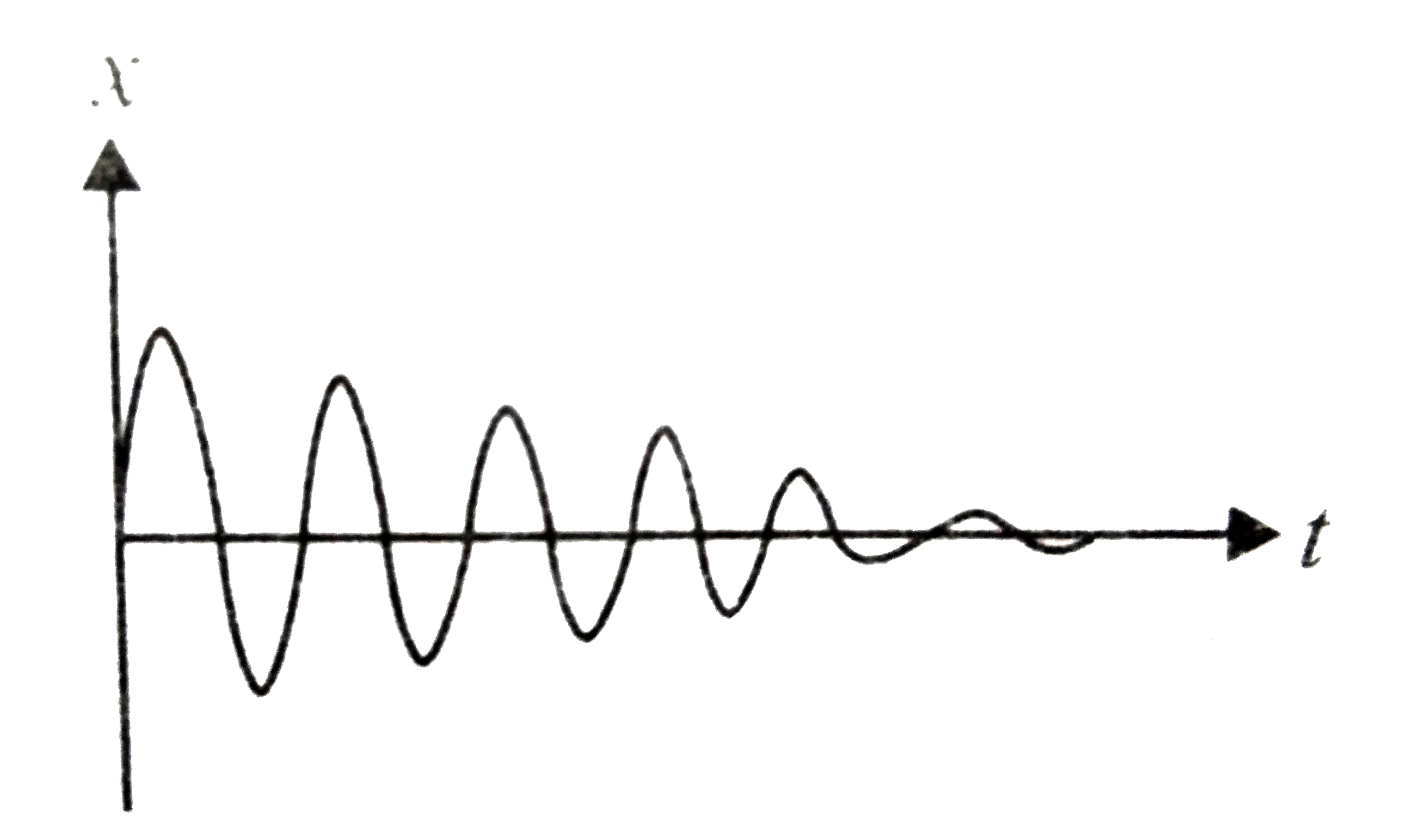 D
D
Figure show the displacement - time graph of a particle moving on the x-axis
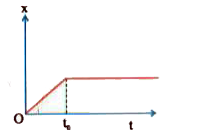 Athe particle is continuously going in positive X directionBthe particle is at restCthe velocity increases up to a time t0 and then becomes constant.Dthe particle moves at constant velocity up to a time t0 and then stops.
Athe particle is continuously going in positive X directionBthe particle is at restCthe velocity increases up to a time t0 and then becomes constant.Dthe particle moves at constant velocity up to a time t0 and then stops.
What does the slope of a work-time graph represent?
View SolutionGraphs(Displacement-time)
View SolutionWhat can be said about velocity of the object if its displacement-time graph is parallel to displacement axis?
View Solution" Find corresponding velocity - time graph for given displacement-time graph "
View Solutionwhat does slope of prosition-time graph represeent for a unitorm motion?
View SolutionFigure shows the displacement time graph of a particle moving on the X-axis

View Solution
