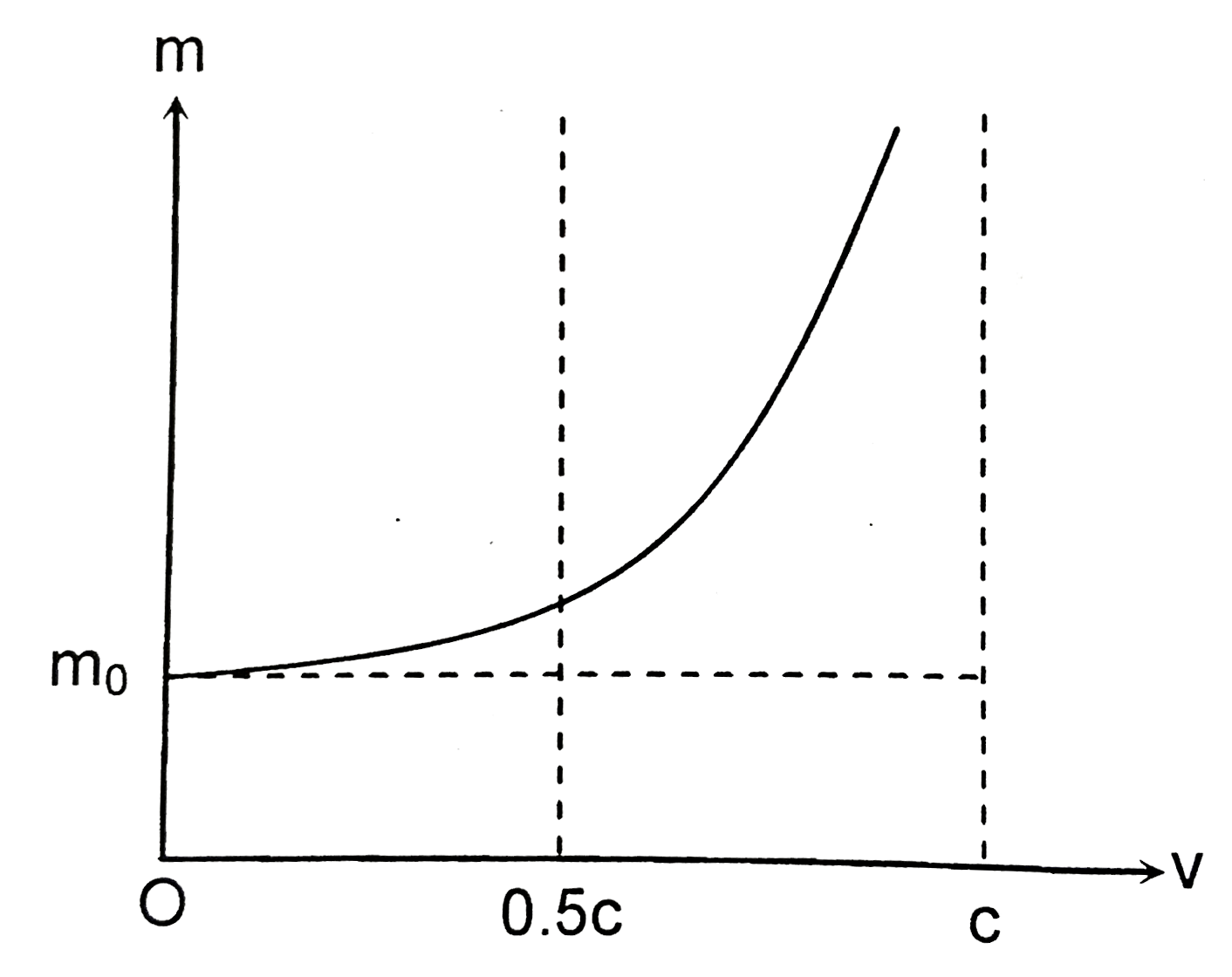
According to Einstein’s theory of relativity, the mass m of a body moving with velocity v is $m = \frac{m_{0}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$ , where $m_{0}$ is the initial mass and c is the speed of light. What happens to m as $v \to c^{-}$ . Why is a left hand limit necessary?

Text Solution

Verified by Experts

The correct Answer is: $1 - \frac{v^{2}}{c^{2}} < 0$

|

Updated on:21/07/2023

Class 11 MATHS DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITY

Topper's Solved these Questions

BOOK - NCERT TAMILCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - Illustration
3videos
DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITY
BOOK - NCERT TAMILCHAPTER - DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITYEXERCISE - EXERCISE 9.1
20videos
DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITY
BOOK - NCERT TAMILCHAPTER - CONIC SECTIONSEXERCISE - Miscellaneous Exercise
8videos
CONIC SECTIONS
BOOK - NCERT TAMILCHAPTER - DIFFERENTIAL CALCULUS-DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION EXERCISE - EXERCISE 10.5
25videos
DIFFERENTIAL CALCULUS-DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION

Similar Questions

Knowledge Check

Question 1 - Select One
According to Einsteins theory of relativity, mass of an object moving with velocity v is
A $m = \frac{m_{0}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$
B $m = \frac{m_{0}}{{(1 - \frac{v^{2}}{c^{2}})}^{\frac{1}{2}}}$
C $m = m_{0} {(1 - \frac{v^{2}}{c^{2}})}^{- \frac{1}{2}}$
Dall of these
Question 2 - Select One
$m = \frac{M}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$
The equation above describes, according to Einstein's theory of relativity, how the mass of an object increase with velocity where m is the mass of moving object, M is the mass the mass the object when it is not moving, v is the velocity of the object relative to a stationary observer, and c is the speed of light. Which of the following expresses v in terms of m, M, and c?
A $c \sqrt{1 - {(\frac{M}{m})}^{2}}$
B $c \sqrt{1 + {(\frac{M}{m})}^{2}}$
C $\sqrt{c^{2} + {(\frac{M}{m})}^{2}}$
D $\sqrt{c^{2} + {(\frac{M}{m})}^{2}} - 1$
Question 3 - Select One
A body of mass m moving with a velocity v strikes a statioinalry body of mass m and sticks to it. What is the speed of the system?
A2v
Bv
C $\frac{v}{2}$
D $\frac{v}{3}$

NCERT TAMIL-DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITY-EXERCISE 9.6 (Choose the correct or the most suitable answer from the given four alternatives)

Home
Ask Doubt
Profile