In a shopping mall there is a hall of cuboid shape with dimension units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find the slopes of the escalator at the turning points.
The correct Answer is:The slope at each turning point is
Topper's Solved these Questions
- TWO DIMENSIONAL ANALYTICAL GEOMETRYBOOK - NCERT TAMILCHAPTER - TWO DIMENSIONAL ANALYTICAL GEOMETRYEXERCISE - EXERCISE 6.3
25 Videos
- TWO DIMENSIONAL ANALYTICAL GEOMETRYBOOK - NCERT TAMILCHAPTER - TWO DIMENSIONAL ANALYTICAL GEOMETRYEXERCISE - EXERCISE 6.4
11 Videos
- TWO DIMENSIONAL ANALYTICAL GEOMETRYBOOK - NCERT TAMILCHAPTER - TWO DIMENSIONAL ANALYTICAL GEOMETRYEXERCISE - EXERCISE 6.1
16 Videos
- TRIGONOMETRYBOOK - NCERT TAMILCHAPTER - TRIGONOMETRYEXERCISE - EXERCISE 3.12
20 Videos
- VECTOR ALGEBRA - I BOOK - NCERT TAMILCHAPTER - VECTOR ALGEBRA - I EXERCISE - EXERCISE 8.5
25 Videos
Similar Questions
A ray of light travelling with a speed c leaves point 1 shown in figure and is reflected to point 2. The ray strikes the reflecting surface at a distance x from point 1. According to Fermat's principle of least time, among all possible paths between two points , the one actually taken by a ray of light is that for which the time taken is the least (In fact there are some cases in which the time taken by a ray is maximum rather than a minimum).
_S01_058_Q01.png)
Find the time for the ray to reach from point 1 to point 2.
View SolutionFind the point on the curve y=3x2+4 at which the tangent is perpendicular to the line whose slope is −16.
View Solution
Knowledge Check
A ray of light travelling with a speed c leaves point 1 shown in figure and is reflected to point 2. The ray strikes the reflecting surface at a distance x from point 1. According to Fermat's principle of least time, among all possible paths between two points , the one actually taken by a ray of light is that for which the time taken is the least (In fact there are some cases in which the time taken by a ray is maximum rather than a minimum).
Find the time for the ray to reach from point 1 to point 2.A√Y21+x2+√(l−x)2+Y22cBlcCY1c+Y2cD2xcFigure given below shows a beam of light converging at point P. When a convex lens of focal length 16cm is introduced in the path of the beam at a place O shown by dotted line such that OP becomes the axis of the lens, the beam converges at a distance x from the lens. The value x will be equal to
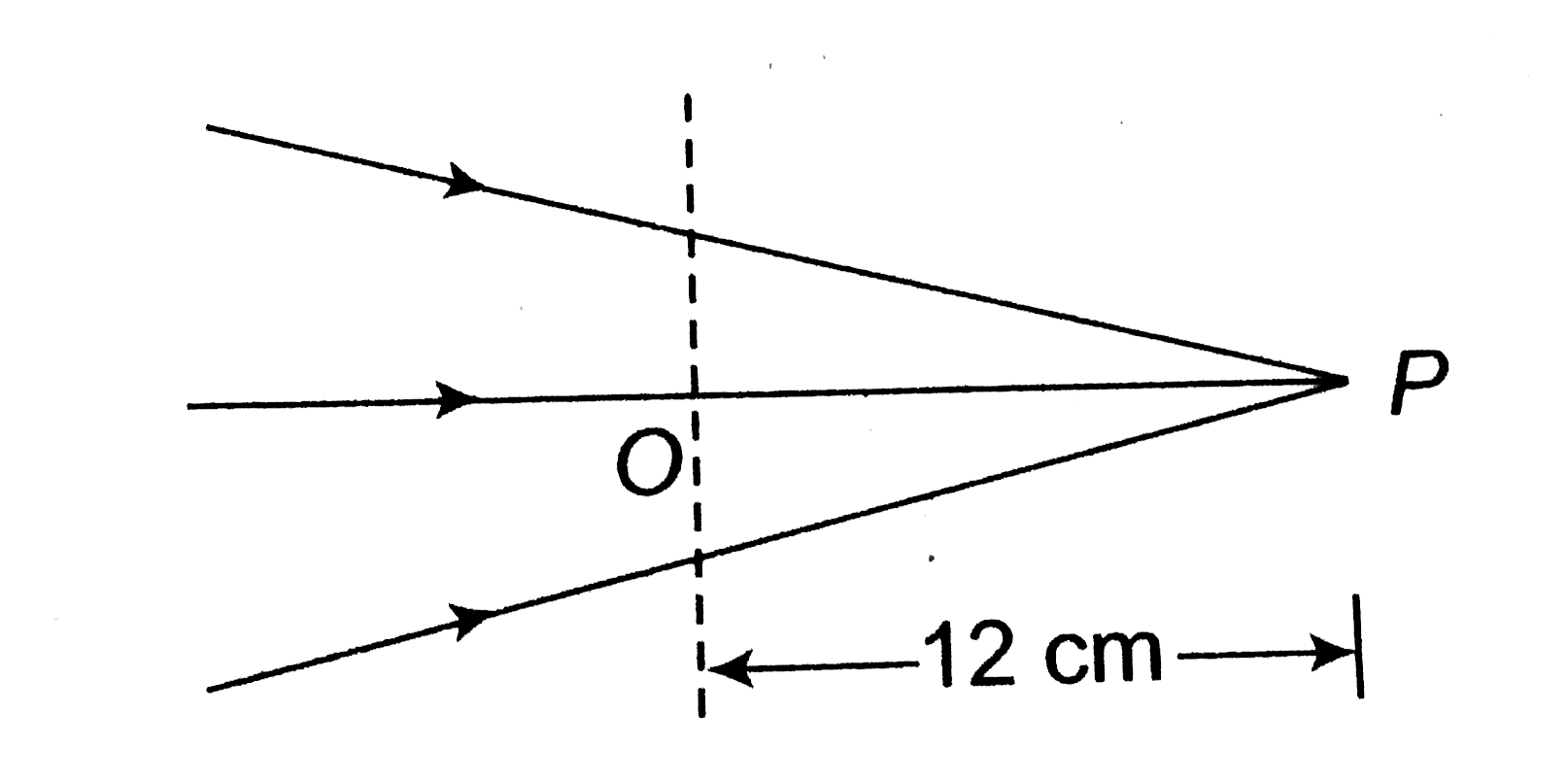A12cmB24cmC36cmD48cm
Figure given below shows a beam of light converging at point P. When a concave lens of focal length 16cm is introduced in the path of the beam at a place O shown by dotted line such that OP becomes the axis of the lens, the beam converges at a distance x from the lens. The value x will be equal to
View SolutionFind the equation of two straight lines which are parallel to x+7y+2=0 and at unit distance from the point (1,−1).
View SolutionA circle C is tangent to the x and y axis in the first quadrant at the points P and Q respectively. BC and AD are parallel tangents to the circle with slope –1. If the points A and B are on the y-axis while C and D are on the x-axis and the area of the figure ABCD is 900 . √2 sq. units then find the radius of the circle.
View Solution(i) Two infinitely long line charges each of linear charge density λ are placed at an angle θ as shown in figure. Find out electric field intensity at a point P, which is at a distance x from point O along angle bisector of line charges.
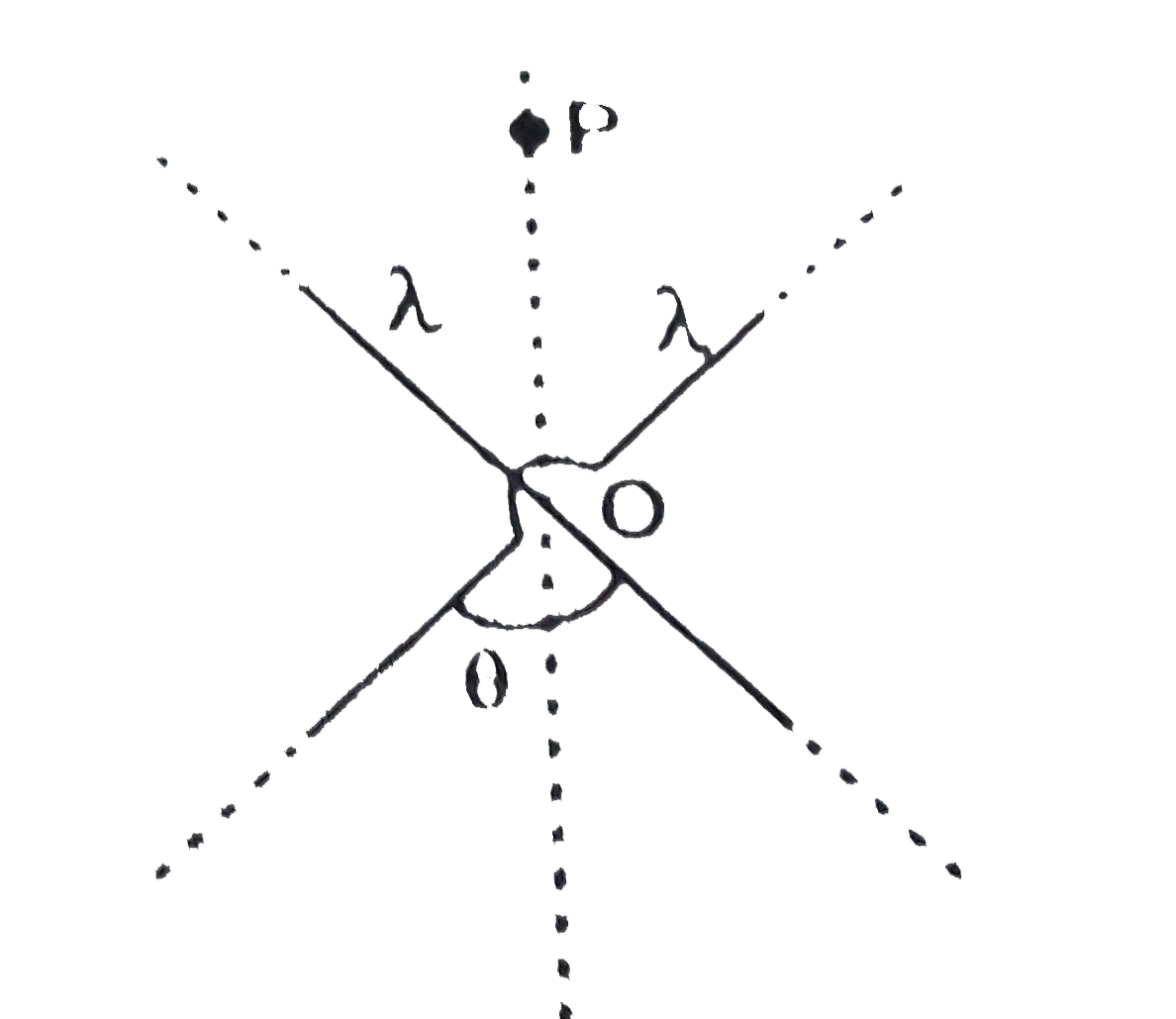
(ii) Repeat the above question if the line charge densities are λ and −λ. as shown in figure.
View Solution(i) Two infinitely long line charges each of linear charge density λ are placed at an angle θ as shown in figure. Find out electric field intensity at a point P, which is at a distance x from point O along angle bisector of line charges.
(ii) Repeat the above question if the line charge densities are λ and −λ. as shown in figure.
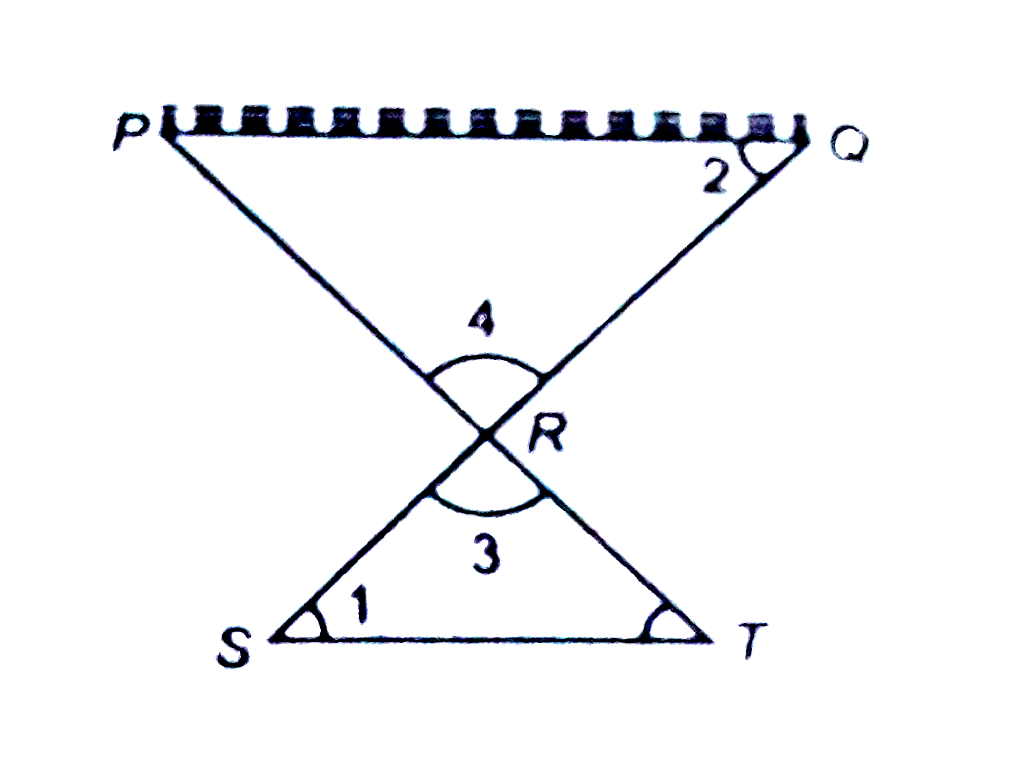
View SolutionDr. Bansal needs to determine the distance PQ across a river in and east-west direction as shown in the adjoining figure. He can't measure this distance directly over the water. So, he selects the point S from where a straight line to point Q stays on land so he can mesure distance. he then moves eastward a distance of 400 m from point S to T , so that the line of sight from point T to P cuts the previous line SQ at R. finally with a long measuring tape. he determines that.
SR = 250 m, QR= 1250 m
Determine if this is enough information to calculate the distance PQ and if so, find PQ and hence find the time taken by a swimmer to cross the river PQ with a uniform speed of 800 m/hr.
View Solution