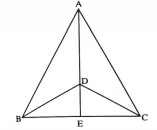
In the fig. AB=AC , D is the point in the interior of $△ A B C$ such that $∠ D B C = ∠ D C B$ . Prove that AD bisects $∠ B A C$ and $△ A B C$
Solution in Punjabi

Video Solution

Answer

Step by step video & image solution for In the fig. AB=AC , D is the point in the interior of triangleABC such that angleDBC=angleDCB. Prove that AD bisects angleBAC and triangleABC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023

Class 9 MATHS TRIANGLES