In Fig.
 ,
,
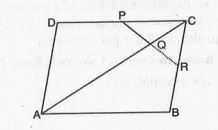
ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.Solution in Punjabi
Step by step video & image solution for In Fig. , ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = 1/4AC. If PQ produced meets BC at R, prove that R is a mid-point of BC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Three angles of a quadrilteral are respectively 50∘ and 110∘ and 100∘ . Find the fourth angles.
View SolutionDefine a trial.
View SolutionDefine
Statistics as a subject.
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionAt point P, the value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_025_Q01.png" width="80%"gt
View SolutionABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ =14AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.
View Solutionएक समान्तर चतुर्भुज ABCD में, P, DC का मध्य बिंदु है तथा एक बिंदु Q भुजा एक पर इस प्रकार है कि CQ=14AC अब PQ को बढ़ाने पर यह BC से बिंदु R पर मिलती है तो सिद्ध कीजिए कि R भुजा BC का मध्य बिंदु है |
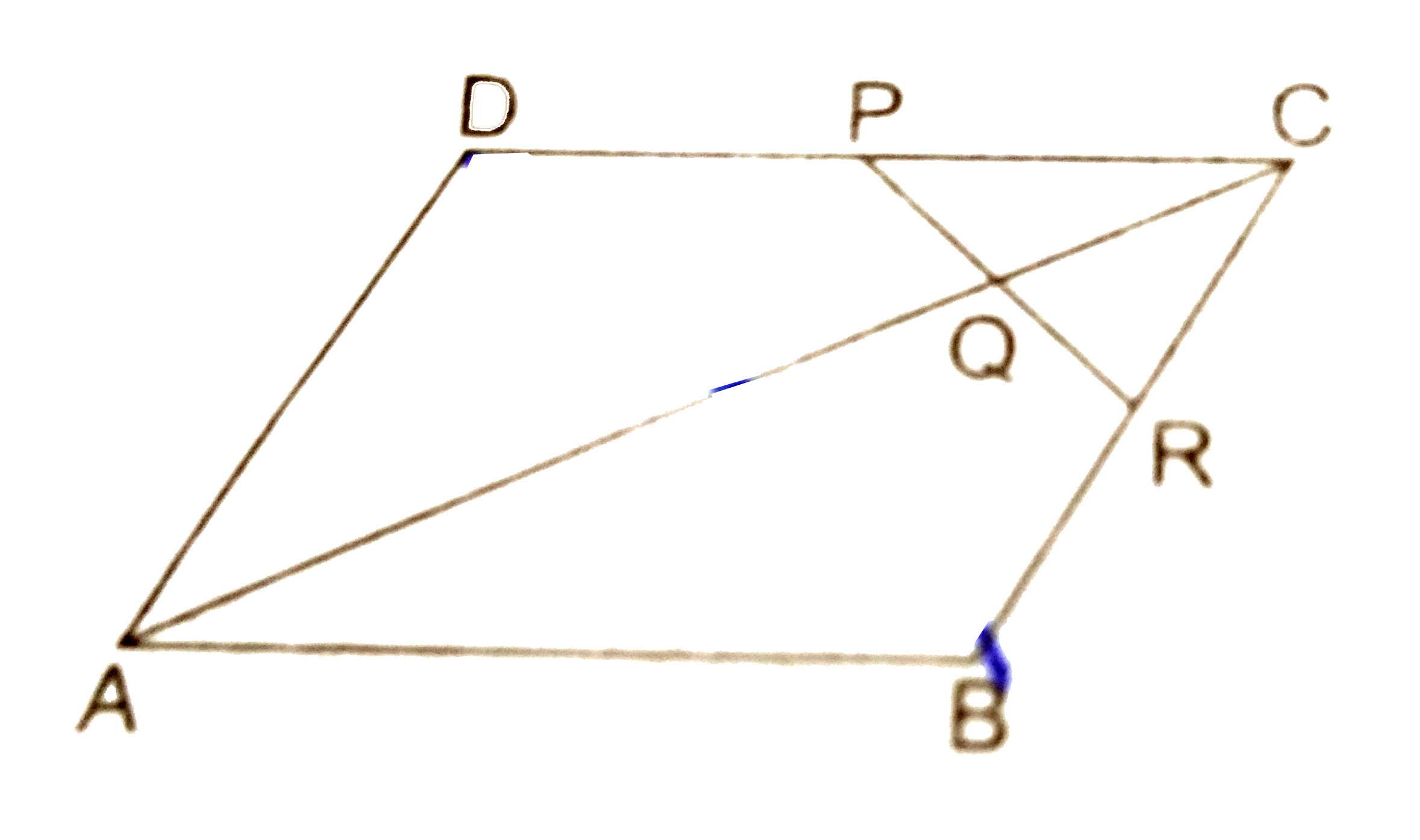
View SolutionIn parallel quadrilateral ABCD, point P is the midpoint of DC and a point Q on AC is positioned such that CQ = (1)/(4) AC If PQ intersects BC at the point R, prove that R will be the midpoint of BC.
View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt
View Solution
